Exam 16: Markov Processes
Exam 1: Introduction63 Questions
Exam 2: An Introduction to Linear Programming66 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution56 Questions
Exam 4: Linear Programming Applications in Marketing, Finance, and Operations Management63 Questions
Exam 5: Advanced Linear Programming Applications46 Questions
Exam 6: Distribution and Network Models70 Questions
Exam 7: Integer Linear Programming61 Questions
Exam 8: Nonlinear Optimization Models51 Questions
Exam 9: Project Scheduling: Pertcpm59 Questions
Exam 10: Inventory Models65 Questions
Exam 11: Waiting Line Models68 Questions
Exam 12: Simulation62 Questions
Exam 13: Decision Analysis97 Questions
Exam 14: Multicriteria Decisions50 Questions
Exam 15: Time Series Analysis and Forecasting63 Questions
Exam 16: Markov Processes49 Questions
Exam 17: Linear Programming: Simplex Method51 Questions
Exam 18: Simplex-Based Sensitivity Analysis and Duality35 Questions
Exam 19: Solution Procedures for Transportation and Assignment Problems44 Questions
Exam 20: Minimal Spanning Tree19 Questions
Exam 21: Dynamic Programming38 Questions
Select questions type
Calculate the steady state probabilities for this transition matrix. 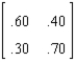
(Short Answer)
4.9/5  (34)
(34)
The fundamental matrix is used to calculate the probability of the process moving into each absorbing state.
(True/False)
4.8/5  (28)
(28)
The medical prognosis for a patient with a certain disease is to recover, to die, to exhibit symptom 1, or to exhibit symptom 2. The matrix of transition probabilities is 
a.What are the absorbing states?
b.What is the probability that a patient with symptom 2 will recover?
a.What are the absorbing states?
b.What is the probability that a patient with symptom 2 will recover?
(Essay)
4.9/5  (30)
(30)
The probability that a system is in a particular state after a large number of periods is
(Multiple Choice)
4.9/5  (38)
(38)
Henry, a persistent salesman, calls North's Hardware Store once a week hoping to speak with the store's buying agent, Shirley. If Shirley does not accept Henry's call this week, the probability she will do the same next week is .35. On the other hand, if she accepts Henry's call this week, the probability she will not do so next week is .20.
a.Construct the transition matrix for this problem.
b.How many times per year can Henry expect to talk to Shirley?
c.What is the probability Shirley will accept Henry's next two calls if she does not accept his call this week?
d.What is the probability of Shirley accepting exactly one of Henry's next two calls if she accepts his call this week?
(Essay)
4.8/5  (35)
(35)
What assumptions are necessary for a Markov process to have stationary transition probabilities?
(Short Answer)
4.8/5  (32)
(32)
Appointments in a medical office are scheduled every 15 minutes. Throughout the day, appointments will be running on time or late, depending on the previous appointment only, according to the following matrix of transition probabilities: 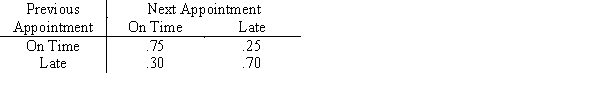
a.The day begins with the first appointment on time. What are the state probabilities for periods 1, 2, 3 and 4?
b.What are the steady state probabilities?
a.The day begins with the first appointment on time. What are the state probabilities for periods 1, 2, 3 and 4?
b.What are the steady state probabilities?
(Essay)
5.0/5  (36)
(36)
For Markov processes having the memoryless property, the prior states of the system must be considered in order to predict the future behavior of the system.
(True/False)
4.9/5  (41)
(41)
A unique matrix of transition probabilities should be developed for each customer.
(True/False)
4.8/5  (30)
(30)
The probability of reaching an absorbing state is given by the
(Multiple Choice)
4.8/5  (30)
(30)
On any particular day an individual can take one of two routes to work. Route A has a 25% chance of being congested, whereas route B has a 40% chance of being congested.
The probability of the individual taking a particular route depends on his previous day's experience. If one day he takes route A and it is not congested, he will take route A again the next day with probability .8. If it is congested, he will take route B the next day with probability .7.
On the other hand, if on a day he takes route B and it is not congested, he will take route B again the next day with probability .9. Similarly if route B is congested, he will take route A the next day with probability .6.
a.Construct the transition matrix for this problem. (HINT: There are 4 states corresponding to the route taken and the congestion. The transition probabilities are products of the independent probabilities of congestion and next day choice.)
b.What is the long-run proportion of time that route A is taken?
(Essay)
4.9/5  (28)
(28)
In Markov analysis, we are concerned with the probability that the
(Multiple Choice)
4.8/5  (29)
(29)
For a situation with weekly dining at either an Italian or Mexican restaurant,
(Multiple Choice)
4.8/5  (30)
(30)
A state i is a transient state if there exists a state j that is reachable from i, but the state i is not reachable from state j.
(True/False)
4.7/5  (24)
(24)
A television ratings company surveys 100 viewers on March 1 and April 1 to find what was being watched at 6:00 p.m. -- the local NBC affiliate's local news, the CBS affiliate's local news, or "Other" which includes all other channels and not watching TV. The results show
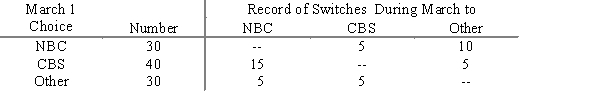
a.What are the numbers in each choice for April 1?
b.What is the transition matrix?
c.What ratings percentages do you predict for May 1?
a.What are the numbers in each choice for April 1?
b.What is the transition matrix?
c.What ratings percentages do you predict for May 1?
(Essay)
4.8/5  (31)
(31)
Showing 21 - 40 of 49
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)