Exam 16: Markov Processes

Accounts receivable have been grouped into the following states: State 1: Paid State 2: Bad debt State 3: 0-30 days old State 4: 31-60 days old Sixty percent of all new bills are paid before they are 30 days old. The remainder of these go to state 4. Seventy percent of all 30 day old bills are paid before they become 60 days old. If not paid, they are permanently classified as bad debts. a.Set up the one month Markov transition matrix. b.What is the probability that an account in state 3 will be paid?

The daily price of a farm commodity is up, down, or unchanged from the day before. Analysts predict that if the last price was down, there is a .5 probability the next will be down, and a .4 probability the price will be unchanged. If the last price was unchanged, there is a .35 probability it will be down and a .35 probability it will be up. For prices whose last movement was up, the probabilities of down, unchanged, and up are .1, .3, and .6. a.Construct the matrix of transition probabilities. b.Calculate the steady state probabilities.

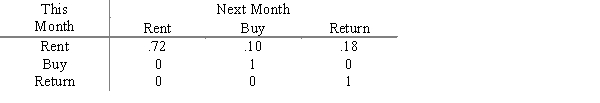
Rent-To-Keep rents household furnishings by the month. At the end of a rental month a customer can: a) rent the item for another month, b) buy the item, or c) return the item. The matrix below describes the month-to-month transition probabilities for 32-inch stereo televisions the shop stocks. ​​ ​ What is the probability that a customer who rented a TV this month will eventually buy it?

Markov processes use historical probabilities.

If a Markov chain has at least one absorbing state, steady-state probabilities cannot be calculated.

The matrix of transition probabilities below deals with brand loyalty to Bark Bits and Canine Chow dog food. ​ a.What are the steady state probabilities? b.What is the probability that a customer will switch brands on the next purchase after a large number of periods?

All Markov chains have steady-state probabilities.

Bark Bits Company is planning an advertising campaign to raise the brand loyalty of its customers to .80. a.The former transition matrix is 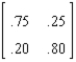What is the new one? b.What are the new steady state probabilities? c.If each point of market share increases profit by $15000, what is the most you would pay for the advertising?

A Markov chain cannot consist of all absorbing states.