Exam 1: Linear Equations in Linear Algebra
Exam 1: Linear Equations in Linear Algebra79 Questions
Exam 2: Matrix Algebra82 Questions
Exam 3: Determinants18 Questions
Exam 4: Vector Spaces47 Questions
Exam 5: Eigenvalues and Eigenvectors20 Questions
Exam 6: Orthogonality and Least Squares44 Questions
Exam 7: Symmetric Matrices and Quadratic Forms25 Questions
Exam 8: The Geometry of Vector Spaces57 Questions
Exam 9: Optimization Online Only55 Questions
Select questions type
Solve the problem.
-Let and .
Define a transformation by . Find , the image of under the transformation .
(Multiple Choice)
4.9/5  (40)
(40)
Determine whether the system is consistent.
- ++=7 -+2=7 5++=11
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-The network in the figure shows the traffic flow (in vehicles per hour)over several one-way streets in the downtown area of a certain city during a typical lunch time. Determine the general flow
Pattern for the network.
In other words, find the general solution of the system of equations that describes the flow. In your
General solution let x4 be free. 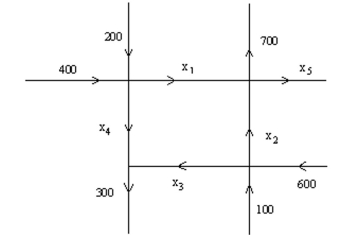
(Multiple Choice)
4.9/5  (39)
(39)
Determine whether the system is consistent.
- +3+2=11 4+9=-12 +7+11=-11
(Multiple Choice)
4.7/5  (30)
(30)
Determine whether the system is consistent.
- 5+2+=-11 2-3-=17 7-=12
(Multiple Choice)
4.9/5  (45)
(45)
Solve the problem.
-Describe all solutions of Ax = b, where and
Describe the general solution in parametric vector form.
(Multiple Choice)
4.8/5  (30)
(30)
The augmented matrix is given for a system of equations. If the system is consistent, find the general solution.
Otherwise state that there is no solution.
-
(Multiple Choice)
4.8/5  (29)
(29)
Determine whether the matrix is in echelon form, reduced echelon form, or neither.
-
(Multiple Choice)
4.8/5  (37)
(37)
Determine whether the matrix is in echelon form, reduced echelon form, or neither.
-
(Multiple Choice)
4.9/5  (40)
(40)
Determine whether the matrix is in echelon form, reduced echelon form, or neither.
-
(Multiple Choice)
4.9/5  (32)
(32)
Solve the problem.
-For what values of h are the given vectors linearly independent?
(Multiple Choice)
4.8/5  (37)
(37)
Describe geometrically the effect of the transformation T.
-Let
Define a transformation by .
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-A company manufactures two products. For $1.00 worth of product A, the company
spends $0.40 on materials, $0.25 on labor, and $0.10 on overhead. For $1.00 worth of
product B, the company spends $0.50 on materials, $0.20 on labor, and $0.10 on overhead.
Let Then a and b represent the ʺcosts per dollar of incomeʺ for the two products.
Evaluate 100a + 400b and give an economic interpretation of the result.
(Essay)
4.9/5  (36)
(36)
Determine whether the system is consistent.
- 4-+3 =12 2+9 =-5 +4+6 =-32
(Multiple Choice)
4.8/5  (38)
(38)
Showing 41 - 60 of 79
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)