Exam 3: Graphs and Functions
Exam 1: Review of Basic Concepts637 Questions
Exam 2: Equations and Inequalities498 Questions
Exam 3: Graphs and Functions531 Questions
Exam 4: Polynomials and Rational Functions517 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Systems and Matrices505 Questions
Exam 7: Arithmetic Sequence: Common Difference and First n Terms570 Questions
Select questions type
Use a graphing calculator to solve the linear equation.
-The graph of is shown in the standard viewing window. Which is the only choice that could possibly be the solution of the equation ?
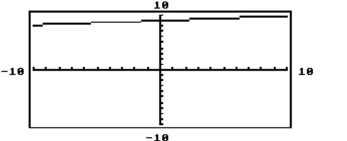
(Multiple Choice)
4.9/5  (29)
(29)
Match the description with the correct symbolic expression.
-a line with a positive slope
(Multiple Choice)
4.9/5  (39)
(39)
Consider the function h as defined. Find functions f and g so tha
-
(Multiple Choice)
4.9/5  (37)
(37)
Find the center-radius form of the equation of the circle.
-center , radius 7
(Multiple Choice)
4.8/5  (38)
(38)
Provide an appropriate response.
-What is the distance from the origin to the point ?
(Multiple Choice)
4.8/5  (37)
(37)
Find the center-radius form of the equation of the circle.
-center , radius
(Multiple Choice)
4.8/5  (30)
(30)
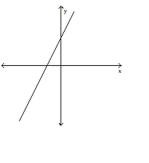
Choose the value which could represent the slope of the line. Assume that the scale on the x-axis is the same as the scale
on the y-axis.
-
(Multiple Choice)
4.8/5  (33)
(33)
Write all linear equations in slope-intercept form.
-In a lab experiment 3 grams of acid were produced in 17 minutes and 18 grams in 45 minutes. Find a linear equation that models the number of grams produced in x minutes.
(Multiple Choice)
4.8/5  (30)
(30)
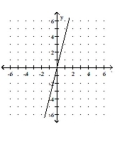
The graph of a linear function f is shown. Write the equation that defines f. Write the equation in slope-intercept form.
-
(Multiple Choice)
4.8/5  (37)
(37)
Write an equation for the line described. Give your answer in slope-intercept form.
-through
(Multiple Choice)
4.7/5  (25)
(25)
An equation that defines y as a function of x is given. Rewrite the equation using function notation f(x).
-
(Multiple Choice)
4.9/5  (43)
(43)
Find the slope of the line satisfying the given conditions.
-through and
(Multiple Choice)
4.8/5  (39)
(39)
An equation that defines y as a function of x is given. Rewrite the equation using function notation f(x).
-
(Multiple Choice)
4.7/5  (35)
(35)
Showing 481 - 500 of 531
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)