Exam 3: Graphs and Functions
Exam 1: Review of Basic Concepts637 Questions
Exam 2: Equations and Inequalities498 Questions
Exam 3: Graphs and Functions531 Questions
Exam 4: Polynomials and Rational Functions517 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Systems and Matrices505 Questions
Exam 7: Arithmetic Sequence: Common Difference and First n Terms570 Questions
Select questions type
Give a rule for the piecewise-defined function. Then give the domain and range.
-
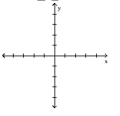
(Multiple Choice)
4.8/5  (35)
(35)
Find the center-radius form of the equation of the circle.
-center , radius 6
(Multiple Choice)
4.8/5  (39)
(39)
Find the slope of the line satisfying the given conditions.
-through and
(Multiple Choice)
4.7/5  (34)
(34)
The figure below shows the graph of a functio e this graph to
-

(Multiple Choice)
4.8/5  (34)
(34)
Consider the function h as defined. Find functions f and g so tha
-
(Multiple Choice)
4.9/5  (30)
(30)
Find the center-radius form of the equation of the circle.
-center (0, 2), radius 4
(Multiple Choice)
4.7/5  (35)
(35)
Suppose a car rental company charges $72 for the first day and $22 for each additional or partial day. Let S(x) represent the cost of renting a car for x days. Find the value of S(5.5).
(Multiple Choice)
4.9/5  (28)
(28)
The charges for renting a moving van are for the first 40 miles and for each additional mile. Assume that a fraction of a mile is rounded up. (i) Determine the cost of driving the van 84 miles. (ii) Find a symbolic representation for a function that computes the cost of driving the van miles, where . (Hint: express as a piecewise-constant function.)
(Multiple Choice)
4.7/5  (32)
(32)
In Country X, the average hourly wage in dollars from 1960 to 2010 can be modeled by Use f to estimate the average hourly wages in 1965, 1985, and 2005.
(Multiple Choice)
5.0/5  (29)
(29)
For the given functions f and g , find the indicated composition.
-
(Multiple Choice)
4.7/5  (35)
(35)
Describe how the graph of the equation relates to the graph of y .
-
![Describe how the graph of the equation relates to the graph of y y = \sqrt [ 3 ] { x } . - f(x)=6(-x)^{3}](https://storage.examlex.com/TB7516/11ecc544_9aea_7fcb_8347_2b828428cbbd_TB7516_11.jpg)
(Multiple Choice)
4.7/5  (36)
(36)
Graph the linear function and give the domain and the range. If the function is a constant function, identify it as such.
-
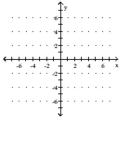
(Multiple Choice)
4.8/5  (39)
(39)
The line graph shows the recorded hourly temperatures in degrees Fahrenheit at an airport. 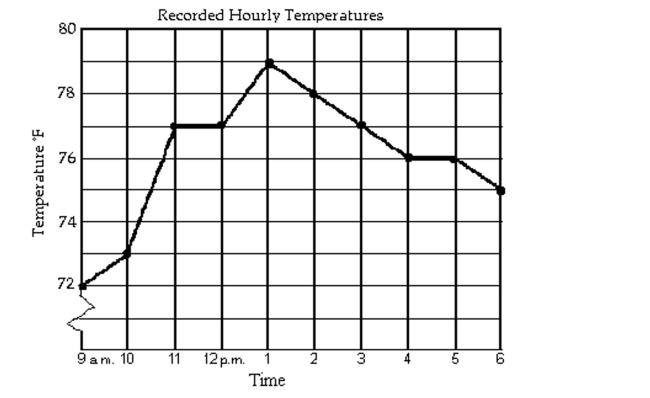 -During which two hour period did the temperature increase the most?
-During which two hour period did the temperature increase the most?
(Multiple Choice)
4.8/5  (38)
(38)
Determine whether the three points are collinear.
-Which one is the graph of ? What is its range?
(Multiple Choice)
5.0/5  (36)
(36)
Find the center-radius form of the circle described or graphed.
-a circle having a diameter with endpoints and
(Multiple Choice)
4.9/5  (38)
(38)
Describe how the graph of the equation relates to the graph
-
(Multiple Choice)
4.8/5  (26)
(26)
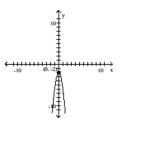
Determine the largest open intervals of the domain over which the function is increasing, decreasing, and constant.
-
(Multiple Choice)
4.8/5  (34)
(34)
Showing 141 - 160 of 531
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)