Exam 9: Analytic Geometry
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Find an equation of the parabola described and state the two points that define the latus rectum.
-Focus at (0, 4); directrix the line y = -4 A) ; latus rectum: and
B) ; latus rectum: and
C) ; latus rectum: and
D) ; latus rectum: and
(Multiple Choice)
4.9/5  (35)
(35)
Find a polar equation for the conic. A focus is at the pole.
- ; directrix is parallel to the polar axis 1 above the pole
(Multiple Choice)
5.0/5  (42)
(42)
Solve the problem.
-A spotlight has a parabolic cross section that is 6 ft wide at the opening and 2.5 ft deep at the vertex. How far from the vertex is the focus? Round answer to two decimal places.
(Multiple Choice)
4.9/5  (38)
(38)
Find a rectangular equation for the plane curve defined by the parametric equations.
-
(Multiple Choice)
4.9/5  (34)
(34)
Rotate the axes so that the new equation contains no xy-term. Graph the new equation.
-
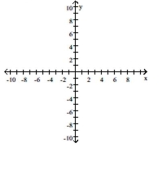
(Multiple Choice)
4.8/5  (41)
(41)
Identify the conic that the polar equation represents. Also, give the position of the directrix.
-
(Multiple Choice)
4.8/5  (41)
(41)
Solve the problem.
-A satellite dish is shaped like a paraboloid of revolution. The signals that emanate from a satellite strike the
surface of the dish and are reflected to a single point, where the receiver is located. If the dish is 8 feet across at
its opening and is 2 feet deep at its center, at what position should the receiver be placed?
(Essay)
4.9/5  (42)
(42)
Find a polar equation for the conic. A focus is at the pole.
- ; directrix is perpendicular to the polar axis 3 to the right of the pole
(Multiple Choice)
4.8/5  (40)
(40)
Find an equation for the hyperbola described.
-center at ; focus at ; vertex at
(Multiple Choice)
4.8/5  (39)
(39)
Find the vertex, focus, and directrix of the parabola with the given equation.
-
(Multiple Choice)
4.9/5  (42)
(42)
Graph the hyperbola.
-Two recording devices are set 2,800 feet apart, with the device at point A to the west of the device at point B. At a point on a line between the devices, 400 feet from point B, a small amount of explosive is detonated. The
Recording devices record the time the sound reaches each one. How far directly north of site B should a second
Explosion be done so that the measured time difference recorded by the devices is the same as that for the first
Detonation?
(Multiple Choice)
4.9/5  (39)
(39)
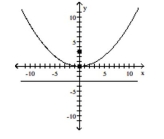
Find the vertex, focus, and directrix of the parabola.
-
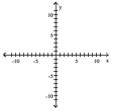 A)
vertex: (0,0) focus: (-3,0) directrix: x=3
A)
vertex: (0,0) focus: (-3,0) directrix: x=3
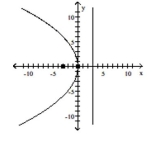 B)
vertex: (0,0) focus: (3,0) directrix: x=-3
B)
vertex: (0,0) focus: (3,0) directrix: x=-3
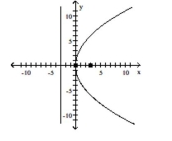 C) vertex:
focus:
directrix:
11ed81f4_181c_1451_a8e7_855e330b9a6b_TB7697_11
D) vertex:
focus:
directrix:
C) vertex:
focus:
directrix:
11ed81f4_181c_1451_a8e7_855e330b9a6b_TB7697_11
D) vertex:
focus:
directrix:
(Multiple Choice)
4.7/5  (44)
(44)
Showing 121 - 140 of 197
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)