Exam 9: Analytic Geometry
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Identify the equation without applying a rotation of axes.
-
(Multiple Choice)
4.8/5  (34)
(34)
Find an equation of the parabola described.
-Focus at (0, 21); directrix the line y = -21 A)
B)
C)
D)
(Multiple Choice)
4.8/5  (41)
(41)
Find an equation for the ellipse described.
-Foci at -intercepts are
(Multiple Choice)
4.8/5  (36)
(36)
Find the vertex, focus, and directrix of the parabola.
-
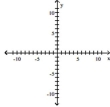 A) vertex:
focus:
directrix:
A) vertex:
focus:
directrix:
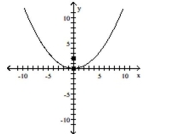 B) vertex:
focus:
directrix:
B) vertex:
focus:
directrix:
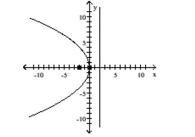 C) vertex:
focus:
directrix:
C) vertex:
focus:
directrix:
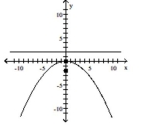 D) vertex:
focus:
directrix:
D) vertex:
focus:
directrix:
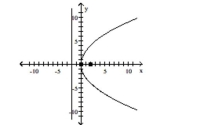
(Multiple Choice)
4.8/5  (45)
(45)
Find an equation for the ellipse described.
-Foci at -intercepts are
(Multiple Choice)
4.7/5  (36)
(36)
Find an equation for the hyperbola described.
-Vertices at ; asymptotes at
(Multiple Choice)
4.8/5  (32)
(32)
Find an equation for the hyperbola described.
-Vertices and asymptotes
(Multiple Choice)
4.7/5  (32)
(32)
Find an equation for the hyperbola described. Graph the equation.
-Center at vertex at focus at
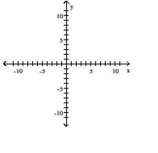
(Multiple Choice)
4.8/5  (30)
(30)
Find an equation for the ellipse described.
-Center at ; focus at ; vertex at
(Multiple Choice)
4.9/5  (40)
(40)
Identify the equation without applying a rotation of axes.
-
(Multiple Choice)
4.8/5  (45)
(45)
Graph the hyperbola.
-A satellite following the hyperbolic path shown in the picture turns rapidly at and then moves closer and closer to the line as it gets farther from the tracking station at the origin. Find the equation that describes the path of the rocket if the center of the hyperbola is at .
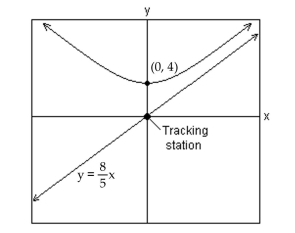
(Multiple Choice)
4.8/5  (31)
(31)
Solve the problem.
-Find parametric equations for an object that moves along the ellipse with the motion described.
The motion begins at , is counterclockwise, and requires 5 seconds for a complete revolution.
(Multiple Choice)
4.8/5  (30)
(30)
Showing 81 - 100 of 197
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)