Exam 9: Analytic Geometry
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Graph the curve whose parametric equations are given.
-
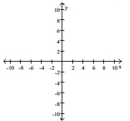 A)
A)
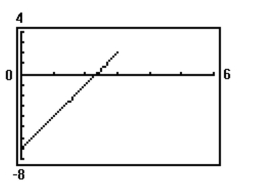 B)
B)
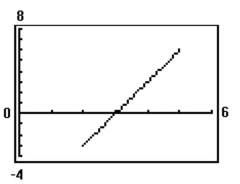 C)
C)
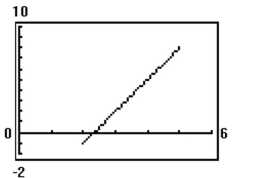 D)
D)
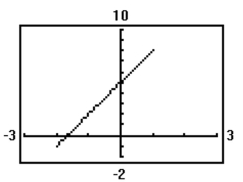
(Multiple Choice)
5.0/5  (29)
(29)
Find a rectangular equation for the plane curve defined by the parametric equations.
-
(Multiple Choice)
4.8/5  (39)
(39)
Identify the conic that the polar equation represents. Also, give the position of the directrix.
-
(Multiple Choice)
4.8/5  (47)
(47)
Rotate the axes so that the new equation contains no xy-term. Discuss the new equati
-
(Multiple Choice)
4.9/5  (30)
(30)
Find an equation for the ellipse described. Graph the equation.
-Center at focus at contains the point
(Multiple Choice)
4.7/5  (39)
(39)
Rotate the axes so that the new equation contains no xy-term. Graph the new equation.
-
(Multiple Choice)
4.9/5  (41)
(41)
Solve the problem.
-A reflecting telescope has a mirror shaped like a paraboloid of revolution. If the distance of the vertex to the focus is 31 feet and the distance across the top of the mirror is 66 inches, how deep is the mirror in the center? A) in.
B) in.
C) in.
D) .
(Multiple Choice)
4.7/5  (38)
(38)
Find an equation of the parabola described.
-Focus at (-3, 0); directrix the line x = 3 A)
B)
C)
D)
(Multiple Choice)
4.9/5  (41)
(41)
Find the vertex, focus, and directrix of the parabola. Graph the equation.
-
 A)
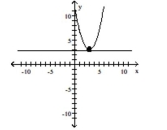
vertex: (3,3) focus: (3,3.25) directrix: y=2.75
A)
vertex: (3,3) focus: (3,3.25) directrix: y=2.75
 B)
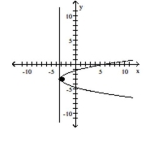
vertex: (-3,-3) focus: (-2.75,-3) directrix: x=-3.25
B)
vertex: (-3,-3) focus: (-2.75,-3) directrix: x=-3.25
 C)
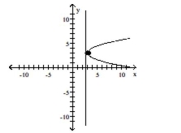
vertex: (3,3) focus: (3.25,3) directrix: x=2.75
C)
vertex: (3,3) focus: (3.25,3) directrix: x=2.75
 D)
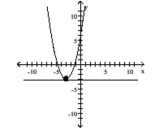
vertex:
focus:
directrix:
D)
vertex:
focus:
directrix:
(Multiple Choice)
4.8/5  (35)
(35)
Graph the hyperbola.
-The roof of a building is in the shape of the hyperbola , where and are in meters. Determine the distance, , the outside walls are apart, if the height of each wall is .
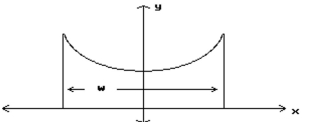
(Multiple Choice)
4.7/5  (37)
(37)
Find the vertex, focus, and directrix of the parabola with the given equation.
-
(Multiple Choice)
4.9/5  (40)
(40)
Rotate the axes so that the new equation contains no xy-term. Discuss the new equati
-
(Multiple Choice)
4.9/5  (31)
(31)
Showing 181 - 197 of 197
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)