Exam 9: Analytic Geometry
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Rotate the axes so that the new equation contains no xy-term. Graph the new equation.
-
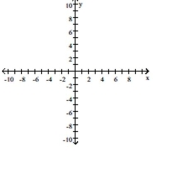
(Multiple Choice)
4.7/5  (31)
(31)
Find an equation of the parabola described.
-Directrix the line y = 3; vertex at (0, 0) A)
B)
C)
D)
(Multiple Choice)
4.8/5  (44)
(44)
Find an equation for the ellipse described.
-Center at ; focus at ; vertex at
(Multiple Choice)
5.0/5  (36)
(36)
Solve the problem.
-A hall 130 feet in length was designed as a whispering gallery. If the ceiling is 25 feet high at the center, how far
from the center are the foci located?
(Short Answer)
4.8/5  (30)
(30)
Find an equation for the ellipse described.
-Vertices at and ; focus at
(Multiple Choice)
4.9/5  (36)
(36)
Find a rectangular equation for the plane curve defined by the parametric equations.
-
(Multiple Choice)
4.9/5  (39)
(39)
Find a polar equation for the conic. A focus is at the pole.
- directrix is perpendicular to the polar axis 2 to the left of the pole
(Multiple Choice)
4.8/5  (34)
(34)
Rotate the axes so that the new equation contains no xy-term. Graph the new equation.
-
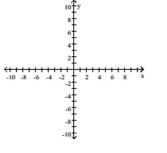
(Multiple Choice)
4.9/5  (40)
(40)
Find the vertex, focus, and directrix of the parabola. Graph the equation.
-
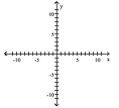 A)
vertex:
focus:
directrix:
A)
vertex:
focus:
directrix:
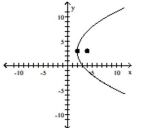 B)
vertex: (-3,-2) focus: (-1,-2) directrix: x=-5
B)
vertex: (-3,-2) focus: (-1,-2) directrix: x=-5
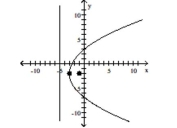 C)
vertex:
focus:
directrix:
C)
vertex:
focus:
directrix:
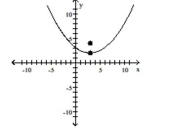 D)
vertex: (-3,-2) focus: (-3,0) directrix: y=-4
D)
vertex: (-3,-2) focus: (-3,0) directrix: y=-4
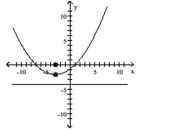
(Multiple Choice)
4.8/5  (38)
(38)
Find an equation for the hyperbola described.
-Vertices at asymptotes at
(Multiple Choice)
4.7/5  (35)
(35)
Rotate the axes so that the new equation contains no xy-term. Graph the new equation.
-
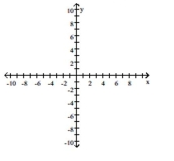
(Multiple Choice)
4.9/5  (38)
(38)
Find the vertex, focus, and directrix of the parabola with the given equation.
-
(Multiple Choice)
4.7/5  (42)
(42)
Solve the problem.
-A sealed-beam headlight is in the shape of a paraboloid of revolution. The bulb, which is placed at the focus, is
3 centimeters from the vertex. If the depth is to be 6 centimeters, what is the diameter of the headlight at its
opening?
(Short Answer)
4.9/5  (47)
(47)
Find an equation for the hyperbola described.
-Vertices at ; foci at
(Multiple Choice)
4.9/5  (43)
(43)
Showing 161 - 180 of 197
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)