Exam 2: Linear and Quadratic Functions
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Graph the function using its vertex, axis of symmetry, and intercepts.
-
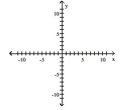 A) vertex
intercepts
A) vertex
intercepts
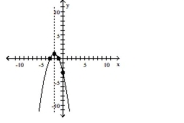 B) vertex
intercepts
B) vertex
intercepts
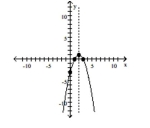 C) vertex
intercepts
C) vertex
intercepts
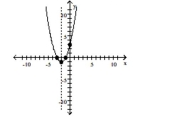 D) vertex
intercepts
D) vertex
intercepts
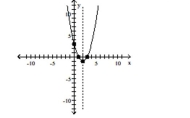
(Multiple Choice)
4.7/5  (25)
(25)
Determine, without graphing, whether the given quadratic function has a maximum value or a minimum value and then
find that value.
-
(Multiple Choice)
4.8/5  (33)
(33)
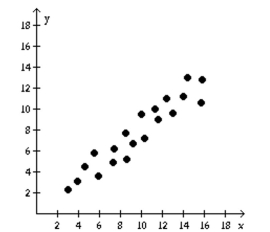
Determine if the type of relation is linear, nonlinear, or none.
-
(Multiple Choice)
4.9/5  (40)
(40)
Solve f(x) = g(x). Find the points of intersection of the graphs of the two functions.
- f(x)=7x+8 g(x)=
(Multiple Choice)
5.0/5  (37)
(37)
Without solving, determine the character of the solutions of the equation.
-
(Multiple Choice)
4.7/5  (26)
(26)
Use a graphing utility to find the equation of the line of best fit. Round to two decimal places, if necessary.
- 3 5 7 15 16 8 11 7 14 20
(Multiple Choice)
4.8/5  (30)
(30)
Solve f(x) = g(x). Find the points of intersection of the graphs of the two functions.
- f(x)=-13x+36 g(x)=2-16x+32 A) x=-,x=
B)
C)
D)
(Multiple Choice)
4.9/5  (31)
(31)
Use a graphing calculator to plot the data and find the quadratic function of best fit.
-Southern Granite and Marble sells granite and marble by the square yard. One of its granite patterns is price sensitive. If the price is too low, customers perceive that it has less quality. If the price is too high, customers
Perceive that it is overpriced. The company conducted a pricing test with potential customers. The following
Data was collected. Use a graphing calculator to plot the data. What is the quadratic function of best fit? Price, x Buyers, B \ 20 30 \ 30 50 \ 40 65 \ 60 75 \ 80 72 \ 100 50 \ 110 25
(Multiple Choice)
4.8/5  (48)
(48)
Find the real zeros of the function. List the x-intercepts of the graph of the function.
-
(Multiple Choice)
4.8/5  (29)
(29)
Determine where the function is increasing and where it is decreasing.
-
(Multiple Choice)
4.7/5  (34)
(34)
Solve the problem.
-The following data represents the number of employees at a company at the start of each year since the company
began. month 1 2 3 4 5 6 7 number 3 172 403 571 823 1061 1194 Find the slope of the line of best fit for the data set and interpret it.
(Essay)
4.8/5  (31)
(31)
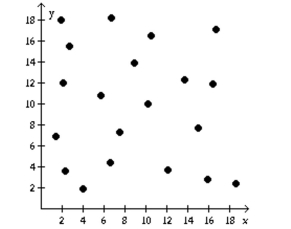
Determine if the type of relation is linear, nonlinear, or none.
-
(Multiple Choice)
4.8/5  (40)
(40)
Determine the average rate of change for the function.
-f(x) = 5x - 3
(Multiple Choice)
4.9/5  (27)
(27)
Solve the problem.
-The revenue achieved by selling graphing calculators is figured to be dollars. The cost of each calculator is . How many graphing calculators must be sold to make a profit (revenue - cost) of at least
(Multiple Choice)
4.8/5  (33)
(33)
Without solving, determine the character of the solutions of the equation.
-
(Multiple Choice)
5.0/5  (39)
(39)
Solve the problem.
-The manufacturer of a CD player has found that the revenue R (in dollars) is when the unit price is p dollars. If the manufacturer sets the price p to maximize revenue, what is the maximum revenue to the nearest whole dollar?
(Multiple Choice)
4.9/5  (30)
(30)
Solve the problem.
-A rock falls from a tower that is 208 ft high. As it is falling, its height is given by the formula How many seconds will it take for the rock to hit the ground (h=0)?
(Multiple Choice)
4.8/5  (37)
(37)
Showing 261 - 280 of 301
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)