Exam 2: Linear and Quadratic Functions
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Determine the slope and y-intercept of the function.
-p(x) = -x - 3
(Multiple Choice)
5.0/5  (36)
(36)
Solve the inequality. Express your answer using interval notation. Graph the solution set.
-

(Multiple Choice)
4.9/5  (35)
(35)
Graph the function using its vertex, axis of symmetry, and intercepts.
-
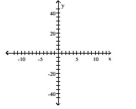 A) vertex (-6,36) intercept (0,72)
A) vertex (-6,36) intercept (0,72)
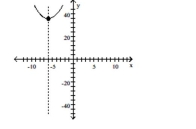 B) vertex (-6,0) intercepts (0,36),(-6,0)
B) vertex (-6,0) intercepts (0,36),(-6,0)
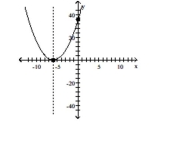 C) vertex (6,36) intercept (0,72)
C) vertex (6,36) intercept (0,72)
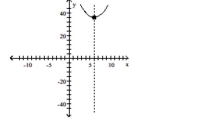 D)vertex
intercepts
D)vertex
intercepts
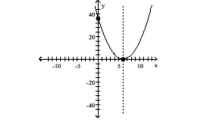
(Multiple Choice)
4.8/5  (34)
(34)
Determine, without graphing, whether the given quadratic function has a maximum value or a minimum value and then
find that value.
-
(Multiple Choice)
4.7/5  (38)
(38)
Solve the problem.
-As part of a physics experiment, Ming drops a baseball from the top of a 310-foot building. To the nearest tenth of a second, for how many seconds will the baseball fall? (Hint: Use the formula h , which gives the
Distance h, in feet, that a free-falling object travels in t seconds.)
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-The following scatter diagram shows heights (in inches) of children and their ages.
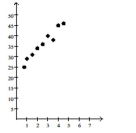 Age (years) Based on this data, how old do you think a child is who is about 39 inches tall?
Age (years) Based on this data, how old do you think a child is who is about 39 inches tall?
(Multiple Choice)
4.8/5  (34)
(34)
Determine where the function is increasing and where it is decreasing.
-
(Multiple Choice)
4.7/5  (38)
(38)
Graph the function f by starting with the graph of y and using transformations (shifting, compressing, stretching,
and/or reflection).
-
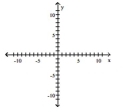 A)
A)
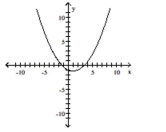 B)
B)
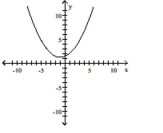 C)
C)
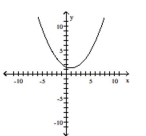 D)
D)
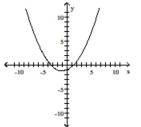
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-The price p and the quantity x sold of a certain product obey the demand equation What quantity x maximizes revenue? What is the maximum revenue?
(Multiple Choice)
4.9/5  (39)
(39)
Plot and interpret the appropriate scatter diagram.
-The table shows the study times and test scores for a number of students. Draw a scatter plot of score versus time
treating time as the independent variable. Study Time () 9 16 21 26 33 36 40 47 Test Score 59 61 64 65 73 74 78 78
(Essay)
4.9/5  (38)
(38)
Find the vertex and axis of symmetry of the graph of the function.
-
(Multiple Choice)
4.9/5  (36)
(36)
Find the zeros of the quadratic function using the Square Root Method. List the x-intercepts of the graph of the function.
-
(Multiple Choice)
4.9/5  (33)
(33)
Without solving, determine the character of the solutions of the equation.
-
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-If a rocket is propelled upward from ground level, its height in meters after t seconds is given by h = -9.8t2 + 78.4t. During what interval of time will the rocket be higher than 147 m?
(Multiple Choice)
4.8/5  (26)
(26)
Use a graphing utility to find the equation of the line of best fit. Round to two decimal places, if necessary.
-Two different tests are designed to measure employee productivity and dexterity. Several employees are randomly selected and tested with these results. Productivity 23 25 28 21 21 25 26 30 34 36 Dexterity 49 53 59 42 47 53 55 63 67 75
(Multiple Choice)
4.8/5  (38)
(38)
Showing 161 - 180 of 301
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)