Exam 2: Linear and Quadratic Functions
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Graph the function using its vertex, axis of symmetry, and intercepts.
-
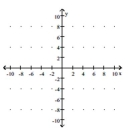 A) vertex
intercept
A) vertex
intercept
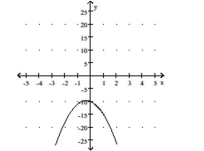 B) vertex
intercept
B) vertex
intercept
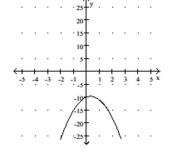 C) vertex
intercept
C) vertex
intercept
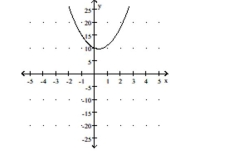 D) vertex
intercept
D) vertex
intercept
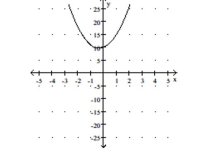
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-A flare fired from the bottom of a gorge is visible only when the flare is above the rim. If it is fired with an initial velocity of , and the gorge is deep, during what interval can the flare be seen?
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-Marty's Tee Shirt & Jacket Company is to produce a new line of jackets with an embroidery of a Great Pyrenees dog on the front. There are fixed costs of $560 to set up for production, and variable costs of $33 per jacket. Write
An equation that can be used to determine the total cost, C(x), encountered by Marty's Company in producing x
Jackets.
(Multiple Choice)
4.7/5  (33)
(33)
Use factoring to find the zeros of the quadratic function. List the x-intercepts of the graph of the function.
-
(Multiple Choice)
4.7/5  (44)
(44)
Use a graphing calculator to plot the data and find the quadratic function of best fit.
-The number of housing starts in one beachside community remained fairly level until 1992 and then began to increase. The following data shows the number of housing starts since 1992 (x = 1). Use a graphing calculator to
Plot a scatter diagram. What is the quadratic function of best fit? Year, x Housing Starts, H 1 200 2 205 3 210 4 240 5 245 6 230 7 220 8 210
(Multiple Choice)
4.9/5  (32)
(32)
Solve the problem.
-Marty's Tee Shirt & Jacket Company is to produce a new line of jackets with a embroidery of a Great Pyrenees dog on the front. There are fixed costs of $650 to set up for production, and variable costs of $39 per jacket. Write
An equation that can be used to determine the total cost, C(x), encountered by Marty's Company in producing x
Jackets, and use the equation to find the total cost of producing 79 jackets.
(Multiple Choice)
4.8/5  (27)
(27)
Find the real zeros, if any, of each quadratic function using the quadratic formula. List the x-intercepts, if any, of the
graph of the function.
-
(Multiple Choice)
4.8/5  (29)
(29)
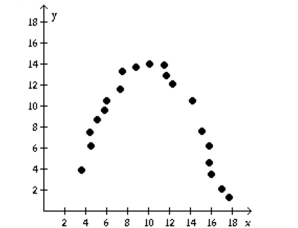
Determine if the type of relation is linear, nonlinear, or none.
-
(Multiple Choice)
4.9/5  (38)
(38)
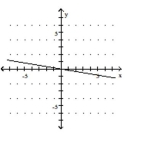
Use the slope and y-intercept to graph the linear function.
-
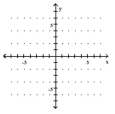 A)
A)
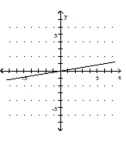
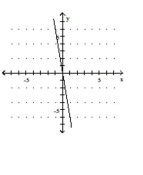 B)
B)
 C)
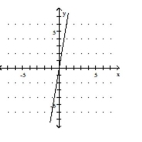
C)
 D)
D)
(Multiple Choice)
4.9/5  (34)
(34)
Graph the function using its vertex, axis of symmetry, and intercepts.
-
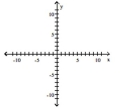 A) vertex
intercepts
A) vertex
intercepts
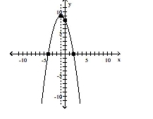 B) vertex
intercepts
B) vertex
intercepts
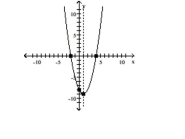 C) vertex
intercepts
C) vertex
intercepts
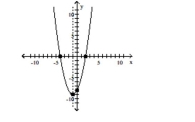 D) vertex
intercepts
D) vertex
intercepts
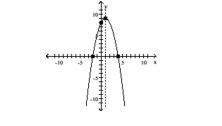
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-To convert a temperature from degrees Celsius to degrees Fahrenheit, you multiply the temperature in degrees Celsius by 1.8 and then add 32 to the result. Express F as a linear function of c. A)
B)
C)
D)
(Multiple Choice)
4.7/5  (33)
(33)
Solve the problem.
-The following data represents the amount of money Tom is saving each month since he graduated from college. month 1 2 3 4 5 6 7 savings \ 52 \ 70 \ 81 \ 91 \ 102 \ 118 \ 132 Using the line of best fit for the data set, predict the amount he will save in the 24th month after graduating from
college.
(Short Answer)
4.8/5  (35)
(35)
Solve the problem.
-The manufacturer of a CD player has found that the revenue R (in dollars) is when the unit price is p dollars. If the manufacturer sets the price p to maximize revenue, what is the maximum revenue to the nearest whole dollar?
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem.
-The price p (in dollars) and the quantity x sold of a certain product obey the demand equation What quantity x maximizes revenue? What is the maximum revenue?
(Multiple Choice)
4.9/5  (21)
(21)
Solve the inequality. Express your answer using interval notation. Graph the solution set.
-

(Multiple Choice)
4.8/5  (33)
(33)
Find the zeros of the quadratic function by completing the square. List the x-intercepts of the graph of the function.
-
(Multiple Choice)
4.8/5  (45)
(45)
Use factoring to find the zeros of the quadratic function. List the x-intercepts of the graph of the function.
-
(Multiple Choice)
4.8/5  (34)
(34)
Showing 181 - 200 of 301
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)