Exam 2: Linear and Quadratic Functions
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Solve the problem.
-A survey of the interest rates earned by Certificates of Deposit (CDs) showed the following percents for the length of time (in years) for holding the CD. Let length of time represent the independent variable and interest
Rate represent the dependent variable. Use a graphing utility to draw a scatter diagram and to find the line of
Best fit. What is the estimate of the interest rate for a CD held for 30 years (to the nearest thousandth)? CD Maturity () Interest rate (\%) 5 8.458 10 8.470 15 8.496 20 8.580 25 8.625
(Multiple Choice)
4.9/5  (25)
(25)
Solve the problem.
-A marina owner wishes to estimate a linear function that relates boat length in feet and its draft (depth of boat below water line) in feet. He collects the following data. Let boat length represent the independent variable and
Draft represent the dependent variable. Use a graphing utility to draw a scatter diagram and to find the line of
Best fit. What is the draft for a boat 60 ft in length (to the nearest tenth)? Boat Length () Draft () 25 2.5 25 2 30 3 30 3.5 45 6 45 7 50 7 50 8
(Multiple Choice)
4.8/5  (33)
(33)
Graph the function f by starting with the graph of y and using transformations (shifting, compressing, stretching,
and/or reflection).
-
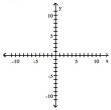 A)
A)
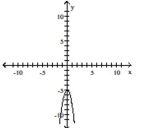 B)
B)
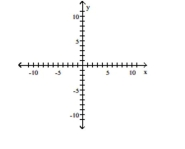 C)
C)
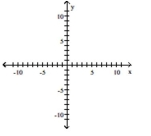 D)
D)
(Multiple Choice)
4.9/5  (39)
(39)
Plot and interpret the appropriate scatter diagram.
-The table gives the times spent watching TV and the grades of several students. Weekly TV (h) 6 12 18 24 30 36 Grade (\%) 92.5 87.5 72.5 77.5 62.5 57.5
Which scatter diagram describes the data and the relationship, if any?
(Multiple Choice)
4.8/5  (43)
(43)
Use a graphing utility to find the equation of the line of best fit. Round to two decimal places, if necessary.
- 10 20 30 40 50 3.9 4.6 5.4 6.9 8.3
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-The price p (in dollars) and the quantity x sold of a certain product obey the demand equation What price should the company charge to maximize revenue?
(Multiple Choice)
4.9/5  (30)
(30)
Use a graphing utility to find the equation of the line of best fit. Round to two decimal places, if necessary.
-Managers rate employees according to job performance and attitude. The results for several randomly selected employees are given below. Performance 59 63 65 69 58 77 76 69 70 64 Attitude 72 67 78 82 75 87 92 83 87 78
(Multiple Choice)
4.9/5  (36)
(36)
Determine, without graphing, whether the given quadratic function has a maximum value or a minimum value and then
find that value.
-
(Multiple Choice)
4.8/5  (31)
(31)
Solve the problem.
-The number of mosquitoes , in millions, in a certain area depends on the June rainfall , in inches: . What rainfall produces the maximum number of mosquitoes?
(Multiple Choice)
4.7/5  (26)
(26)
Solve the problem.
-Identify the scatter diagram of the relation that appears linear. A)
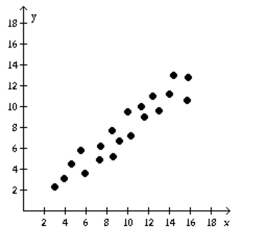 B)
B)
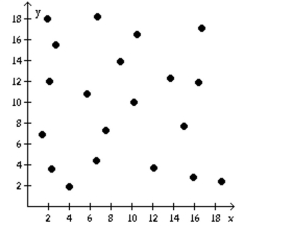 C)
C)
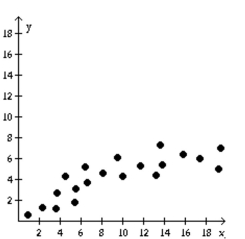 D)
D)
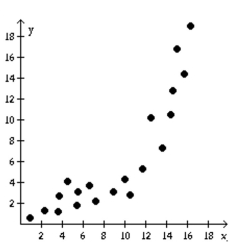
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-A developer wants to enclose a rectangular grassy lot that borders a city street for parking. If the developer has 276 feet of fencing and does not fence the side along the street, what is the largest area that can be enclosed? A)
B)
C)
D)
(Multiple Choice)
4.8/5  (32)
(32)
Use the slope and y-intercept to graph the linear function.
-
 A)
A)
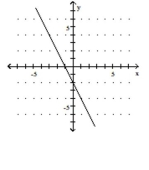 B)
B)
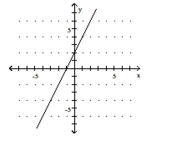 C)
C)
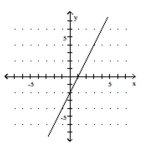 D)
D)
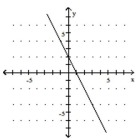
(Multiple Choice)
4.8/5  (37)
(37)
Determine, without graphing, whether the given quadratic function has a maximum value or a minimum value and then
find that value.
-
(Multiple Choice)
4.7/5  (34)
(34)
Solve the problem.
-A projectile is fired from a cliff 300 feet above the water at an inclination of 45° to the horizontal, with a muzzle velocity of 300 feet per second. The height h of the projectile above the water is given by ,
Where x is the horizontal distance of the projectile from the base of the cliff. How far from the base of the cliff is
The height of the projectile a maximum?
(Multiple Choice)
4.8/5  (43)
(43)
Use a graphing utility to find the equation of the line of best fit. Round to two decimal places, if necessary.
- 24 26 28 30 32 15 13 20 16 24
(Multiple Choice)
4.8/5  (32)
(32)
Graph the function. State whether it is increasing, decreasing, or constant..
-
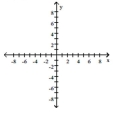 A) constant
A) constant
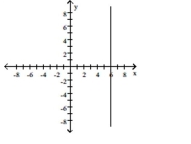 B) constant
B) constant
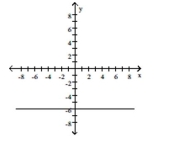 C) decreasing
C) decreasing
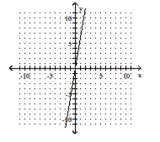 D) constant
D) constant
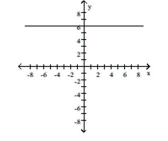
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-You have 348 feet of fencing to enclose a rectangular region. What is the maximum area?
(Multiple Choice)
4.8/5  (34)
(34)
Showing 241 - 260 of 301
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)