Exam 2: Linear and Quadratic Functions
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Solve the problem.
-If an object is dropped off of a tower, the velocity, V, of the object after t seconds can be obtained by multiplying t by 32 and adding 10 to the result. Express V as a linear function of t. A)
B)
C)
D)
(Multiple Choice)
4.7/5  (43)
(43)
Solve the problem.
-The price p and the quantity x sold of a certain product obey the demand equation What price should the company charge to maximize revenue?
(Multiple Choice)
4.9/5  (35)
(35)
Use the slope and y-intercept to graph the linear function.
-
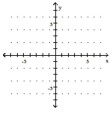 A)
A)
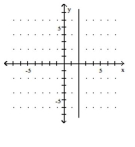 B)
B)
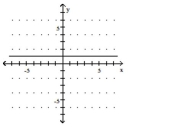 C)
C)
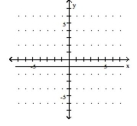 D)
D)
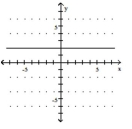
(Multiple Choice)
4.7/5  (34)
(34)
Determine where the function is increasing and where it is decreasing.
-
(Multiple Choice)
4.9/5  (37)
(37)
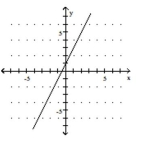
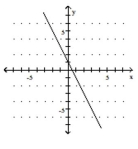
Use the slope and y-intercept to graph the linear function.
-
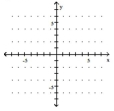 A)
A)
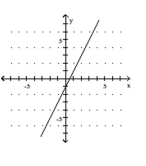 B)
B)
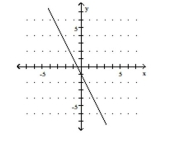 C)
C)
 D)
D)
(Multiple Choice)
4.8/5  (43)
(43)
Use a graphing utility to find the equation of the line of best fit. Round to two decimal places, if necessary.
- 2 3 7 8 10 2 4 4 6 6
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-If an object is dropped from a tower, then the velocity, V (in feet per second), of the object after t seconds can be obtained by multiplying t by 32 and adding 10 to the result. Find V as a linear function of t, and use this
Function to evaluate V(7.4), the velocity of the object at time t = 7.4 seconds.
(Multiple Choice)
4.8/5  (41)
(41)
Solve the problem.
-In a certain city, the cost of a taxi ride is computed as follows: There is a fixed charge of $2.40 as soon as you get in the taxi, to which a charge of $1.90 per mile is added. Find an equation that can be used to determine the cost, C(x), of an x-mile taxi ride.
(Multiple Choice)
4.8/5  (38)
(38)
Find the zeros of the quadratic function using the Square Root Method. List the x-intercepts of the graph of the function.
-
(Multiple Choice)
5.0/5  (37)
(37)
Solve the problem.
-You have 64 feet of fencing to enclose a rectangular plot that borders on a river. If you do not fence the side along the river, find the length and width of the plot that will maximize the area.
(Multiple Choice)
4.9/5  (23)
(23)
Use a graphing calculator to plot the data and find the quadratic function of best fit.
-A small manufacturing firm collected the following data on advertising expenditures (in thousands of dollars) and total revenue (in thousands of dollars). Advertising, Total Revenue, 25 6430 28 6432 31 6434 32 6434 34 6434 39 6431 40 6432 45 6420
Find the quadratic function of best fit.
(Multiple Choice)
4.7/5  (43)
(43)
Solve the problem.
-A rock falls from a tower that is 117.6 m high. As it is falling, its height is given by the formula How many seconds will it take for the rock to hit the ground (h=0)?
(Multiple Choice)
4.8/5  (37)
(37)
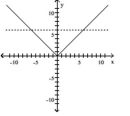
Solve.
-If (solid line)and (dashed line), find when and when .
(Multiple Choice)
4.9/5  (40)
(40)
Solve the problem.
-The following data represents the number of employees at a company at the start of each year since the company
began. month 1 2 3 4 5 6 7 number 3 172 403 571 823 1061 1194 Using the line of best fit for the data set, predict the number of employees at the start of the 10th year.
(Short Answer)
4.7/5  (38)
(38)
Determine, without graphing, whether the given quadratic function has a maximum value or a minimum value and then
find that value.
-
(Multiple Choice)
4.7/5  (24)
(24)
Solve the problem.
-Northwest Molded molds plastic handles which cost $0.20 per handle to mold. The fixed cost to run the molding machine is $5,253 per week. If the company sells the handles for $3.20 each, how many handles must
Be molded and sold weekly to break even?
(Multiple Choice)
4.9/5  (41)
(41)
Solve the problem.
-A projectile is thrown upward so that its distance above the ground after seconds is . After how many seconds does it reach its maximum height?
(Multiple Choice)
4.8/5  (41)
(41)
Showing 281 - 300 of 301
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)