Exam 2: Linear and Quadratic Functions
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
Solve the problem.
-The owner of a video store has determined that the profits P of the store are approximately given by , where x is the number of videos rented daily. Find the maximum profit to the nearest dollar.
(Multiple Choice)
4.8/5  (38)
(38)
Find the vertex and axis of symmetry of the graph of the function.
-
(Multiple Choice)
4.7/5  (42)
(42)
Solve the inequality. Express your answer using interval notation. Graph the solution set.
-

(Multiple Choice)
4.7/5  (32)
(32)
Solve the problem.
-A coin is tossed upward from a balcony high with an initial velocity of . During what interval of time will the coin be at a height of at least ? .)
(Multiple Choice)
4.9/5  (47)
(47)
Plot a scatter diagram.
- 15 21 36 46 58 70 71 84 95 10 23 42 45 68 55 63 96 85
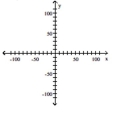 A)
A)
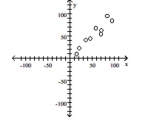 B)
B)
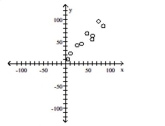 C)
C)
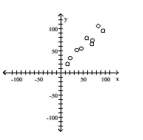 D)
D)
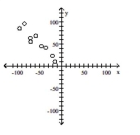
(Multiple Choice)
4.9/5  (29)
(29)
Solve the problem.
-A coin is tossed upward from a balcony high with an initial velocity of . During what interval of time will the coin be at a height of at least ?
(Multiple Choice)
4.8/5  (37)
(37)
Graph the function f by starting with the graph of y and using transformations (shifting, compressing, stretching,
and/or reflection).
-
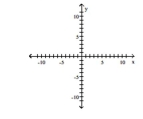 A)
A)
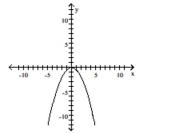 B)
B)
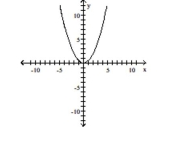 C)
C)
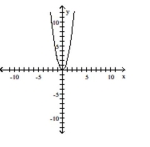 D)
D)
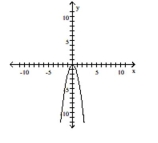
(Multiple Choice)
4.8/5  (44)
(44)
Determine where the function is increasing and where it is decreasing.
-
(Multiple Choice)
4.8/5  (38)
(38)
Graph the function using its vertex, axis of symmetry, and intercepts.
-
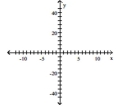 A) vertex (3,-9) intercept (0,-18)
A) vertex (3,-9) intercept (0,-18)
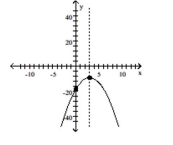 B) vertex (3,9) intercepts (0,0),(6,0)
B) vertex (3,9) intercepts (0,0),(6,0)
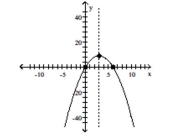 C) vertex
intercepts
C) vertex
intercepts
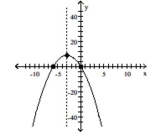 D) vertex
intercept
D) vertex
intercept
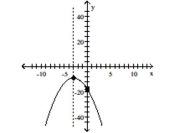
(Multiple Choice)
4.7/5  (36)
(36)
Use a graphing utility to find the equation of the line of best fit. Round to two decimal places, if necessary.
- 2 3 7 8 10 3 4 4 5 6
(Multiple Choice)
4.9/5  (48)
(48)
Solve the inequality. Express your answer using interval notation. Graph the solution set.
-

(Multiple Choice)
4.8/5  (35)
(35)
Graph the function using its vertex, axis of symmetry, and intercepts.
-
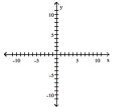 A) vertex
intercepts
A) vertex
intercepts
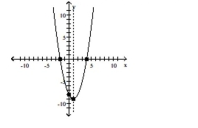 B) vertex
intercepts
B) vertex
intercepts
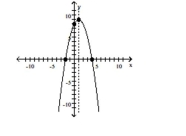 C) vertex
intercepts
C) vertex
intercepts
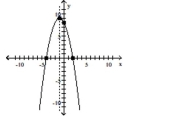 D) vertex
intercepts
D) vertex
intercepts
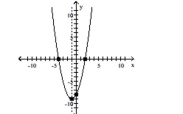
(Multiple Choice)
4.9/5  (33)
(33)
Showing 81 - 100 of 301
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)