Question 1

Find $F _ { .05 }$ where $v _ { 1 } = 8$ and $v _ { 2 } = 11$.

Accepted Answer

A)  $4.74$ 
B)  $3.66$ 
C)  $2.30$ 
D)  $2.95$ 
A)  $4.74$ 
B)  $3.66$ 
C)  $2.30$ 
D)  $2.95$

Question 2

An experiment has been conducted at a university to compare the mean number of study
hours expended per week by student athletes with the mean number of hours expended
by non athletes. A random sample of 55 athletes produced a mean equal to 20.6 hours
studied per week and a standard deviation equal to 5.5 hours. A second random sample of
200 non athletes produced a mean equal to 23.5 hours per week and a standard deviation
equal to 4 hours. How many students would need to be sampled in order to estimate the
difference in means to within 1.5 hours with probability 95%?

Accepted Answer

To determine the sample size n

Question 3

Consider the following set of salary data: $\begin{array}{lrr}
\hline & \text { Men (1) } & \text { Women (2) } \
\hline \text { Sample Size } & 100 & 80 \
\text { Mean } & \$ 12,850 & \$ 13,000 \
\text { Standard Deviation } & \$ 345 & \$ 500 \
\hline
\end{array}$

Suppose the test statistic turned out to be $z = - 1.20$ (not the correct value). Find a two-tailed $p$-value for this test statistic.

Accepted Answer

A)  .6151 
B) . 3849 
C) . 1151 
D)  .2302 
A)  .6151 
B) . 3849 
C) . 1151 
D)  .2302

Question 4

A confidence interval for $\left( \mu _ { 1 } - \mu _ { 2 } \right)$ is $( - 5,8 )$. Which of the following inferences is correct?

Accepted Answer

A)  $\mu _ { 1 } = \mu _ { 2 }$ 
B)  $\mu _ { 1 }  \mu _ { 2 }$ 
D)  no significant difference between means 
A)  $\mu _ { 1 } = \mu _ { 2 }$ 
B)  $\mu _ { 1 }  \mu _ { 2 }$ 
D)  no significant difference between means

Question 5

The screen below shows the $95 \%$ confidence interval for $\left( \mu _ { 1 } - \mu _ { 2 } \right)$.

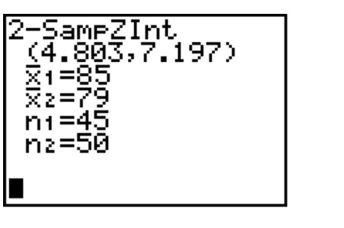What does the interval suggest about the relationship between $\mu _ { 1 }$ and $\mu _ { 2 }$ ?

Accepted Answer

The answer of The screen below shows the $95 \%$...

Question 6

Suppose it desired to compare two physical education training programs for
preadolescent girls. A total of 242 girls are randomly selected, with 121 assigned to each
program. After three 6-week periods on the program, each girl is given a fitness test that
yields a score between 0 and 100. The means and variances of the scores for the two
groups are shown in the table. $$\begin{array}{l}
\begin{array} { l | c | c | c } 
& n & \bar { x } & s ^ { 2 } \
\hline \text { Program 1 } & 121 & 78.3 & 201.8 \
\text { Program 2 } & 121 & 75.5 & 259.1
\end{array}\
\text { Test to determine if the variances of the two programs differ. Use } \alpha = .05 \text {. }
\end{array}$$

Accepted Answer

To determine if the variances of the two

Question 7

A marketing study was conducted to compare the variation in the age of male and female purchasers of a certain product. Random and independent samples were selected for both male
And female purchasers of the product. The sample data is shown here:

Identify the rejection region to that should be used to determine if the variation in the female ages exceeds the variation in the male ages when testing at $\alpha = 0.05$.

Accepted Answer

A)  $\mathrm { F } > 1.93$ 
B)  $\mathrm { F } > 2.04$ 
C)  $\mathrm { F } > 1.74$ 
D)  $\mathrm { F } > 2.12$ 
A)  $\mathrm { F } > 1.93$ 
B)  $\mathrm { F } > 2.04$ 
C)  $\mathrm { F } > 1.74$ 
D)  $\mathrm { F } > 2.12$

Question 8

Consider the following set of salary data: $$\begin{array} { l r r } 
\hline & \text { Men (1) } & \text { Women (2) } \
\hline \text { Sample Size } & 100 & 80 \
\text { Mean } & \$ 12,850 & \$ 13,000 \
\text { Standard Deviation } & \$ 345 & \$ 500 \
\hline
\end{array}$$ What assumptions are necessary to perform a test for the difference in population means?

Accepted Answer

A) The two samples were independently selected from the populations of men and women. 
B) The population variances of salaries for men and women are equal. 
C) Both of the target populations have approximately normal distributions. 
D) All of the above are necessary. 
A) The two samples were independently selected from the populations of men and women. 
B) The population variances of salaries for men and women are equal. 
C) Both of the target populations have approximately normal distributions. 
D) All of the above are necessary.

Question 9

A paired difference experiment has 75 pairs of observations. What is the rejection region for testing $H _ { a } : \mu _ { d } > 0$ ? Use $\alpha = .01$.

Accepted Answer

The reject

Question 10

Data was collected from CEOs of companies within both the low-tech industry and the consumer products industry. The following printout compares the mean return-to-pay ratios between CEOs
In the low tech industry with CEOs in the consumer products industry. HYPOTHESIS: MEAN X = MEAN Y

If we conclude that the mean return-to-pay ratios of the consumer products and low tech CEOs are equal when, in fact, a difference really does exist between the means, we would be making a

Accepted Answer

A)  Type I error 
B)  Type III error 
C)  Type II error 
D)  correct decision 
A)  Type I error 
B)  Type III error 
C)  Type II error 
D)  correct decision

Question 11

Which of the following represents the ratio of variances?

Accepted Answer

A)  $\frac { \mu _ { 1 } } { \mu _ { 2 } }$ 
B)  $\frac { p _ { 1 } } { p _ { 2 } }$ 
C)  $p _ { 1 } - p _ { 2 }$ 
D)  $\frac { \sigma _ { 1 } ^ { 2 } } { \sigma _ { 2 } ^ { 2 } }$ 
A)  $\frac { \mu _ { 1 } } { \mu _ { 2 } }$ 
B)  $\frac { p _ { 1 } } { p _ { 2 } }$ 
C)  $p _ { 1 } - p _ { 2 }$ 
D)  $\frac { \sigma _ { 1 } ^ { 2 } } { \sigma _ { 2 } ^ { 2 } }$

Question 12

Calculate the degrees of freedom associated with a small-sample test of hypothesis for $\left( \mu _ { 1 } { } ^ { \prime } \mu _ { 2 } \right)$, assuming $\sigma _ { 1 } ^ { 2 } \neq \sigma _ { 2 } 2$ and $n _ { 1 } = 13 , n _ { 2 } = 12 , s _ { 1 } = 1.3 , s _ { 2 } = 1.5$.

Accepted Answer

A)  23 
B)  11 
C)  12 
D)  25 
A)  23 
B)  11 
C)  12 
D)  25

Question 13

A paired difference experiment produced the following results. $$n _ { d } = 40 , \bar { x } _ { 1 } = 18.4 , \bar { x } _ { 2 } = 19.7 , \bar { d } = - 1.3 , s _ { d } { } ^ { 2 } = 5$$
Perform the appropriate test to determine whether there is sufficient evidence to conclude that $\mu _ { 1 } ! \mu _ { 2 }$ using $\alpha = .10$.

Accepted Answer

The test statistic is @#LAT-DLM&.
The re

Question 14

Which supermarket has the lowest prices in town? All claim to be cheaper, but an independent agency recently was asked to investigate this question. The agency randomly selected 100 items
Common to each of two supermarkets (labeled A and B)and recorded the prices charged by each
Supermarket. The summary results are provided below:
$$\begin{array} { l l r } 
\bar { x } \mathrm {~A} = 2.09 & \bar { x } \mathrm {~B} = 1.99 & \bar { d } = .10 \
\mathrm {~s} _ { \mathrm { A } } = 0.22 & \mathrm {~s} _ { \mathrm { B } } = 0.19 & s _ { d } = .03
\end{array}$$
Assuming a matched pairs design, which of the following assumptions is necessary for a confidence interval for the mean difference to be valid?

Accepted Answer

A)  None of these assumptions are necessary. 
B)  The samples are randomly and independently selected. 
C)  The population variances must be equal. 
D)  The population of paired differences has an approximate normal distribution. 
A)  None of these assumptions are necessary. 
B)  The samples are randomly and independently selected. 
C)  The population variances must be equal. 
D)  The population of paired differences has an approximate normal distribution.

Question 15

A consumer protection agency is comparing the work of two electrical contractors. The agency plans to inspect residences in which each of these contractors has done the wiring in order to
Estimate the difference in the proportions of residences that are electrically deficient. Suppose the
Proportions of residences with deficient work are expected to be about .7 for both contractors.
How many homes should be sampled in order to estimate the difference in proportions using a
95% confidence interval of width .3?

Accepted Answer

A)  $n _ { 1 } = n _ { 2 } = 36$ 
B)  $n _ { 1 } = n _ { 2 } = 240$ 
C)  $n _ { 1 } = \mathrm { n } _ { 2 } = 144$ 
D)  $n _ { 1 } = n _ { 2 } = 72$ 
A)  $n _ { 1 } = n _ { 2 } = 36$ 
B)  $n _ { 1 } = n _ { 2 } = 240$ 
C)  $n _ { 1 } = \mathrm { n } _ { 2 } = 144$ 
D)  $n _ { 1 } = n _ { 2 } = 72$

Question 16

The FDA is comparing the mean caffeine contents of two brands of cola. Independent random samples of 6-oz. cans of each brand were selected and the caffeine content of each can determined.
The study provided the following summary information. $\begin{array}{lrr}
\hline & \text { Brand A } & \text { Brand B } \
\hline \text { Sample size } & 15 & 10 \
\text { Mean } & 18 & 20 \
\text { Variance } & 1.2 & 1.5 \
\hline
\end{array}$

How many cans of each soda would need to be sampled in order to estimate the difference in the mean caffeine content to within .5 with $95 \%$ reliability?

Accepted Answer

A)  $n _ { 1 } = n _ { 2 } = 57$ 
B)  $n _ { 1 } = n _ { 2 } = 21$ 
C)  $n _ { 1 } = n _ { 2 } = 18$ 
D)  $n _ { 1 } = n _ { 2 } = 42$ 
A)  $n _ { 1 } = n _ { 2 } = 57$ 
B)  $n _ { 1 } = n _ { 2 } = 21$ 
C)  $n _ { 1 } = n _ { 2 } = 18$ 
D)  $n _ { 1 } = n _ { 2 } = 42$

Question 17

A cola manufacturer invited consumers to take a blind taste test. Consumers were asked to decide which of two sodas they preferred. The manufacturer was also interested in what factors played a
Role in taste preferences. Below is a printout comparing the taste preferences of men and women. HYPOTHESIS: PROP. $X =$ PROP. Y
SAMPLES SELECTED FROM soda(brand1,brand2)
 
Suppose the manufacturer wanted to test to determine if the males preferred its brand more than the females. Using the test statistic given, compute the appropriate $p$-value for the test.

Accepted Answer

A)  .4681 
B) . 2119 
C)  0170 
D) . 0340 
A)  .4681 
B) . 2119 
C)  0170 
D) . 0340

Question 18

A paired difference experiment yielded $\mathrm { n } _ { \mathrm { d } }$ pairs of observations. For the given case, what is the rejection region for testing $\mathrm { H } _ { 0 } : \mu _ { \mathrm { d } } = 9$ against Ha: $\mu _ { \mathrm { d } } \neq 9$ ?
$$\mathrm { n } _ { \mathrm { d } } = 13 , \alpha = 0.05$$

Accepted Answer

A)  $t > 1.782$ 
B)  $t > 2.179$ 
C)  $| t | > 2.160$ 
D)  $| t | > 2.179$ 
A)  $t > 1.782$ 
B)  $t > 2.179$ 
C)  $| t | > 2.160$ 
D)  $| t | > 2.179$

Question 19

Independent random samples selected from two normal populations produced the
following sample means and standard deviations. $\begin{array}{ll}
\text { Sample 1 } & \text { Sample } 2 \
n_{1}=14 & n_{2}=11 \
\overline{x_{1}}=7.1 & \bar{x}_{2}=8.4 \
s_{1}=2.3 & s_{2}=2.9
\end{array}$

Find and interpret the $95 \%$ confidence interval for $\left( \mu _ { 1 } - \mu _ { 2 } \right)$.

Accepted Answer

The confidence inter

Question 20

Using paired differences removes sources of variation that tend to inflate $$\sigma ^ { 2 } .$$

Accepted Answer

A) True 
 B)False

Find $F _ { .05 }$ where $v _ { 1 } = 8$ and $v _ { 2 } = 11$ .

Consider the following set of salary data: Men (1) Women (2) Sample Size 100 80 Mean \ 12,850 \ 13,000 Standard Deviation \ 345 \ 500 Suppose the test statistic turned out to be $z = - 1.20$ (not the correct value). Find a two-tailed $p$ -value for this test statistic.

A confidence interval for $\left( \mu _ { 1 } - \mu _ { 2 } \right)$ is $( - 5,8 )$ . Which of the following inferences is correct?

Consider the following set of salary data: Men (1) Women (2) Sample Size 100 80 Mean \ 12,850 \ 13,000 Standard Deviation \ 345 \ 500 What assumptions are necessary to perform a test for the difference in population means?

A paired difference experiment has 75 pairs of observations. What is the rejection region for testing $H _ { a } : \mu _ { d } > 0$ ? Use $\alpha = .01$ .

Which of the following represents the ratio of variances?

Calculate the degrees of freedom associated with a small-sample test of hypothesis for $\left( \mu _ { 1 } { } ^ { \prime } \mu _ { 2 } \right)$ , assuming $\sigma _ { 1 } ^ { 2 } \neq \sigma _ { 2 } 2$ and $n _ { 1 } = 13 , n _ { 2 } = 12 , s _ { 1 } = 1.3 , s _ { 2 } = 1.5$ .

Independent random samples selected from two normal populations produced the following sample means and standard deviations. Sample 1 Sample 2 =14 =11 =7.1 =8.4 =2.3 =2.9 Find and interpret the $95 \%$ confidence interval for $\left( \mu _ { 1 } - \mu _ { 2 } \right)$ .

Using paired differences removes sources of variation that tend to inflate $\sigma ^ { 2 } .$

Statistics, Data, and Statistical Thinking

Methods for Describing Sets of Data

Probability

Discrete Random Variables

Continuous Random Variables

Sampling Distributions

Inferences Based on a Single Sample: Estimation With Confidence Intervals

Inferences Based on a Single

Analysis of Variance: Comparing More Than Two Means

Simple Linear Regression

Multiple Regression and Model Building

Categorical Data Analysis

Nonparametric Statistics Available Online

Filters

Exam 9: Inferences Based on Two Samples: Confidence Intervals and Tests of Hypotheses

Find F.05F _ { .05 }F.05​ where v1=8v _ { 1 } = 8v1​=8 and v2=11v _ { 2 } = 11v2​=11 .

Consider the following set of salary data: Men (1) Women (2) Sample Size 100 80 Mean \ 12,850 \ 13,000 Standard Deviation \ 345 \ 500 Suppose the test statistic turned out to be z=−1.20z = - 1.20z=−1.20 (not the correct value). Find a two-tailed ppp -value for this test statistic.

A confidence interval for (μ1−μ2)\left( \mu _ { 1 } - \mu _ { 2 } \right)(μ1​−μ2​) is (−5,8)( - 5,8 )(−5,8) . Which of the following inferences is correct?

The screen below shows the 95%95 \%95% confidence interval for (μ1−μ2)\left( \mu _ { 1 } - \mu _ { 2 } \right)(μ1​−μ2​) . What does the interval suggest about the relationship between μ1\mu _ { 1 }μ1​ and μ2\mu _ { 2 }μ2​ ?

Consider the following set of salary data: Men (1) Women (2) Sample Size 100 80 Mean \ 12,850 \ 13,000 Standard Deviation \ 345 \ 500 What assumptions are necessary to perform a test for the difference in population means?

A paired difference experiment has 75 pairs of observations. What is the rejection region for testing Ha:μd>0H _ { a } : \mu _ { d } > 0Ha​:μd​>0 ? Use α=.01\alpha = .01α=.01 .

Which of the following represents the ratio of variances?

Using paired differences removes sources of variation that tend to inflate σ2.\sigma ^ { 2 } .σ2.

Statistics, Data, and Statistical Thinking

Methods for Describing Sets of Data

Probability

Discrete Random Variables

Continuous Random Variables

Sampling Distributions

Inferences Based on a Single Sample: Estimation With Confidence Intervals

Inferences Based on a Single

Analysis of Variance: Comparing More Than Two Means

Simple Linear Regression

Multiple Regression and Model Building

Categorical Data Analysis

Nonparametric Statistics Available Online

Filters

Find $F _ { .05 }$ where $v _ { 1 } = 8$ and $v _ { 2 } = 11$ .

Consider the following set of salary data: Men (1) Women (2) Sample Size 100 80 Mean \ 12,850 \ 13,000 Standard Deviation \ 345 \ 500 Suppose the test statistic turned out to be $z = - 1.20$ (not the correct value). Find a two-tailed $p$ -value for this test statistic.

A confidence interval for $\left( \mu _ { 1 } - \mu _ { 2 } \right)$ is $( - 5,8 )$ . Which of the following inferences is correct?

A paired difference experiment has 75 pairs of observations. What is the rejection region for testing $H _ { a } : \mu _ { d } > 0$ ? Use $\alpha = .01$ .

Using paired differences removes sources of variation that tend to inflate $\sigma ^ { 2 } .$