Exam 9: Inferences Based on Two Samples: Confidence Intervals and Tests of Hypotheses

Salary data were collected from CEOs in the consumer products industry and CEOs in the telecommunication industry. The data were analyzed using a software package in order to Compare mean salaries of CEOs in the two industries. HYPOTHESIS: MEAN X = MEAN Y SAMPLES SELECTED FROM SALARY What of the following assumptions is necessary to perform the test described above?

A researcher is investigating which of two newly developed automobile engine oils is better at prolonging the life of an engine. Since there are a variety of automobile engines, 20 different engine Types were randomly selected and were tested using each of the two engine oils. The number of Hours of continuous use before engine breakdown was recorded for each engine oil. Based on the Information provided, what type of analysis will yield the most useful information?

The screens below show the results of a test of 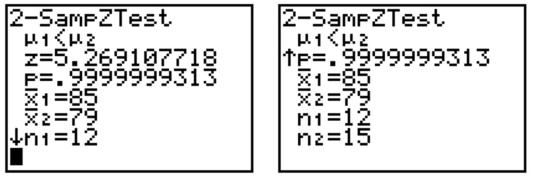$H _ { 0 } : \left( \mu _ { 1 } - \mu _ { 2 } \right) = 0$ against $H _ { a } : \left( \mu _ { 1 } - \mu _ { 2 } \right) \neq 0$ Comment on the validity of the results.

Find $F _ { .10 }$ where $v _ { 1 } = 20$ and $v _ { 2 } = 40$ .

In order to compare the means of two populations, independent random samples of 225 observations are selected from each population with the following results. Sample 1 Sample 2 =478 =481 =14.2 =11.2 Test the null hypothesis $H _ { 0 } : \left( \mu _ { 1 } - \mu _ { 2 } \right) = 0$ against the alternative hypothesis $H _ { \mathrm { a } } : \left( \mu _ { 1 } - \mu _ { 2 } \right) \neq 0$ using $\alpha = .10$ . Give the significance level, and interpret the result.

Given $v _ { 1 } = 9$ and $v _ { 2 } = 5$ , find $P ( F > 6.68 )$ .

Assume that $\sigma _ { 1 } ^ { 2 } = \sigma _ { 2 } ^ { 2 } = \sigma ^ { 2 }$ . Calculate the pooled estimator of $\sigma ^ { 2 }$ for $s _ { 1 } ^ { 2 } = .88$ , $s _ { 2 } ^ { 2 } = 1.01 , n _ { 1 } = 10$ , and $n _ { 2 } = 12$ .

The owners of an industrial plant want to determine which of two types of fuel (gas or electricity) will produce more useful energy at a lower cost. The cost is measured by plant investment per Delivered quad ($ invested /quadrillion BTUs). The smaller this number, the less the industrial Plant pays for delivered energy. Suppose we wish to determine if there is a difference in the Average investment/quad between using electricity and using gas. Our null and alternative Hypotheses would be:

University administrators are trying to decide where to build a new parking garage on campus. The state legislature has budgeted just enough money for one parking structure on campus. The administrators have determined that the parking garage will be built either by the college of engineering or by the college of business. To help make the final decision, the university has randomly and independently asked students from each of the two colleges to estimate how long they usually take to find a parking spot on campus (in minutes). Based on their sample, the following $95 \%$ confidence interval (for $\mu _ { \mathrm { e } } - \mu _ { \mathrm { b } }$ ) was created $- ( 4.20,10.20 )$ . What conclusion can the university make about the population mean parking times based on this confidence interval?

An inventor has developed a new spray coating that is designed to improve the wear of bicycle tires. To test the new coating, the inventor randomly selects one of the two tires on each of 50 Bicycles to be coated with the new spray. The bicycle is then driven for 100 miles and the amount Of the depth of the tread left on the two bicycle tires is measured (in millimeters). It is desired to Determine whether the new spray coating improves the wear of the bicycle tires. The data and Summary information is shown below: Bicycle Coated Tire (C) Non-Coated Tire (N) 1 1.452 0.785 2 1.634 0.844 + 1 + 50 1.211 0.954 Use the summary data to calculate the test statistic to determine if the new spray coating improves the mean wear of the bicycle tires.

A new weight-reducing technique, consisting of a liquid protein diet, is currently undergoing tests by the Food and Drug Administration (FDA) before its introduction into the market. The weights of a random sample of five people are recorded before they are introduced to the liquid protein diet. The five individuals are then instructed to follow the liquid protein diet for 3 weeks. At the end of this period, their weights (in pounds) are again recorded. The results are listed in the table. Let $\mu _ { 1 }$ be the true mean weight of individuals before starting the diet and let $\mu _ { 2 }$ be the true mean weight of individuals after 3 weeks on the diet. Person Weight Before Diet Weight After Diet 1 146 139 2 191 186 3 184 181 4 193 187 5 200 196 Summary information is as follows: $\bar { d } = 5 , s _ { d } = 1.58$ . Test to determine if the diet is effective at reducing weight. Use $\alpha = .10$ .

Two surgical procedures are widely used to treat a certain type of cancer. To compare the success rates of the two procedures, random samples of surgical patients were obtained and the numbers of patients who showed no recurrence of the disease after a 1-year period were recorded. The data are shown in the table. n Number of Successes Procedure A 100 78 Procedure B 100 92 How large a sample would be necessary in order to estimate the difference in the true success rates to within .10 with 95% reliability?

Calculate the degrees of freedom associated with a small-sample test of hypothesis for $\left( \mu _ { 1 } { } ^ { \prime } \mu _ { 2 } \right)$ , assuming $\sigma _ { 1 } { } ^ { 2 } = \sigma _ { 2 } { } ^ { 2 }$ and $n _ { 1 } = n _ { 2 } = 12$ .

Which of the following represents the difference in two population proportions?

A confidence interval for $\left( \mu _ { 1 } - \mu _ { 2 } \right)$ is $( 5,8 )$ . Which of the following inferences is correct?

Data was collected from CEOs of companies within both the low-tech industry and the consumer products industry. The following printout compares the mean return-to-pay ratios between CEOs In the low-tech industry with CEOs in the consumer products industry. HYPOTHESIS: MEAN X = MEAN Y Using the printout, which of the following assumptions is not necessary for the test to be valid?

The data for a random sample of five paired observations are shown below. 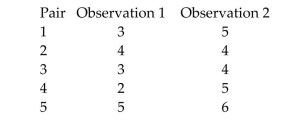a. Calculate the difference between each pair of observations by subtracting observation 2 from observation 1. Use the differences to calculate $\bar { d }$ and $s _ { d }$ . b. Calculate the means $\bar { x } _ { 1 }$ and $\bar { x } _ { 2 }$ of each column of observations. Show that $\bar { d } " \bar { x } _ { 1 } - \bar { x } _ { 2 }$ . c. Form a $90 \%$ confidence interval for $\mu _ { D }$ .

Which of the following represents the difference in two population means?

A paired difference experiment yielded $\mathrm { n } _ { \mathrm { d } }$ pairs of observations. For the given case, what is the rejection region for testing $\mathrm { H } _ { 0 } : \mu _ { \mathrm { d } } = 15$ against Ha: $\mu _ { \mathrm { d } } < 15$ ? $\mathrm { n } _ { \mathrm { d } } = 19 , \alpha = 0.01$