Exam 9: Inferences Based on Two Samples: Confidence Intervals and Tests of Hypotheses

Assume that $\sigma _ { 1 } ^ { 2 } = \sigma _ { 2 } ^ { 2 } = \sigma ^ { 2 }$ . Calculate the pooled estimator of $\sigma ^ { 2 }$ for $s _ { 1 } ^ { 2 } = 50$ , $s _ { 2 } ^ { 2 } = 57$ , and $n _ { 1 } = n _ { 2 } = 18$ .

A paired difference experiment yielded $\mathrm { n } _ { \mathrm { d } }$ pairs of observations. For the given case, what is the rejection region for testing $\mathrm { H } _ { 0 } : \mu _ { \mathrm { d } } = 9$ against $\mathrm { Ha } ^ { \mathrm { a } } \mu _ { \mathrm { d } } > 9$ ? $\mathrm { n } _ { \mathrm { d } } = 12 , \alpha = 0.01$

Calculate the degrees of freedom associated with a small-sample test of hypothesis for $\left( \mu _ { 1 } { } ^ { \prime } \mu _ { 2 } \right)$ , assuming $\sigma _ { 1 } { } ^ { 2 } \neq \sigma _ { 2 } ^ { 2 }$ and $n _ { 1 } = n _ { 2 } = 20$ .

Independent random samples from normal populations produced the results shown below. Sample 1: $5.8,5.1,3.9,4.5,5.4$ Sample 2: 4.4, 6.1, 5.2, $5.7$ a. Calculate the pooled estimator of $\sigma ^ { 2 }$ . b. Test $\mu _ { 1 } < \mu _ { 2 }$ using $\alpha = .10$ . c. Find a $90 \%$ confidence interval for $\left( \mu _ { 1 } - \mu _ { 2 } \right)$ .

A paired difference experiment has 15 pairs of observations. What is the rejection region for testing $H _ { a } : \mu _ { d } > 0$ ? Use $\alpha = .05$ .

Suppose you want to estimate the difference between two population proportions correct to within 0.03 with probability 0.90. If prior information suggests that p1 ≈ 0.4 and p2 ≈ 0.8, and you want to Select independent random samples of equal size from the populations, how large should the Sample sizes be?

When blood levels are low at an area hospital, a call goes out to local residents to give blood. The blood center is interested in determining which sex - males or females - is more likely to respond. Random, independent samples of 60 females and 100 males were each asked if they would be Willing to give blood when called by a local hospital. A success is defined as a person who Responds to the call and donates blood. The goal is to compare the percentage of the successes Between the male and female responses. What type of analysis should be used?

In a controlled laboratory environment, a random sample of 10 adults and a random sample of 10 children were tested by a psychologist to determine the room temperature that each person finds Most comfortable. The data are summarized below: Sample Mean Sample Variance Adults (1) 77. 4.5 Children (2) 74. 2.5 If the psychologist wished to test the hypothesis that children prefer warmer room temperatures than adults, which set of hypotheses would he use?

The data for a random sample of six paired observations are shown below. 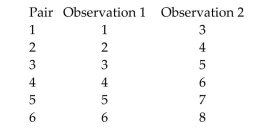a. Calculate the difference between each pair of observations by subtracting observation 2 from observation 1. Use the differences to calculate $s d ^ { 2 }$ . b. Calculate the standard deviations $s _ { 1 } ^ { 2 }$ and $s _ { 2 } ^ { 2 }$ of each column of observations. Then find pooled estimate of the variance $s p ^ { 2 }$ . c. Comparing $s d ^ { 2 }$ and $s p ^ { 2 }$ , explain the benefit of a paired difference experiment.

A marketing study was conducted to compare the mean age of male and female purchasers of a certain product. Random and independent samples were selected for both male and female Purchasers of the product. It was desired to test to determine if the mean age of all female Purchasers exceeds the mean age of all male purchasers. The sample data is shown here: Female: n = 10, sample mean = 50.30, sample standard deviation = 13.215 Male: n = 10, sample mean = 39.80, sample standard deviation = 10.040 Which of the following assumptions must be true in order for the pooled test of hypothesis to be Valid? I. Both the male and female populations of ages must possess approximately normal probability Distributions. II. Both the male and female populations of ages must possess population variances that are Equal. III. Both samples of ages must have been randomly and independently selected from their Respective populations.

The FDA is comparing the mean caffeine contents of two brands of cola. Independent random samples of 6-oz. cans of each brand were selected and the caffeine content of each can determined. The study provided the following summary information. Brand A Brand B Sample size 15 10 Mean 18 20 Variance 1.2 1.5 How many cans of each soda would need to be sampled in order to estimate the difference in the mean caffeine content to within . 10 with $90 \%$ reliability?

Consider the following set of salary data: Men (1) Women (2) Sample Size 100 80 Mean \ 12,850 \ 13,000 Standard Deviation \ 345 \ 500 Calculate the appropriate test statistic for a test about $\mu _ { 1 } ^ { \prime } \mu _ { 2 }$ .

A government housing agency is comparing home ownership rates among several immigrant groups. In a sample of 235 families who emigrated to the U.S. from Eastern Europe five years ago, 165 now own homes. In a sample of 195 families who emigrated to the U.S. from Pacific islands five years ago, 125 now own homes. Write a 95% confidence interval for the difference in home ownership rates between the two groups. Based on the confidence interval, can you conclude that there is a significant difference in home ownership rates in the two groups of immigrants?

Calculate the degrees of freedom associated with a small-sample test of hypothesis for $\left( \mu _ { 1 } { } ^ { \prime } \mu _ { 2 } \right)$ , assuming $\sigma _ { 1 } ^ { 2 } = \sigma _ { 2 } 2$ and $n _ { 1 } = n _ { 2 } = 16$ .

We are interested in comparing the average supermarket prices of two leading colas. Our sample was taken by randomly selecting eight supermarkets and recording the price of a six-pack of each Brand of cola at each supermarket. The data are shown in the following table: 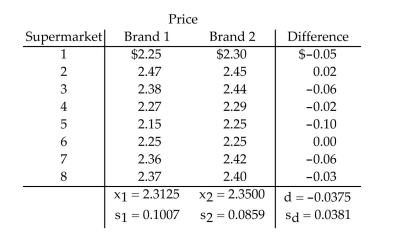Find a $98 \%$ confidence interval for the difference in mean price of brand 1 and brand 2 .

We sampled 100 men and 100 women and asked: ʺDo you think the environment is a major concern?ʺ Of those sampled, 67 women and 53 men responded that they believed it is. For the Confidence interval procedure to work properly, what additional assumptions must be satisfied?

The owners of an industrial plant want to determine which of two types of fuel (gas or electricity) will produce more useful energy at a lower cost. The cost is measured by plant investment per delivered quad (\$ invested /quadrillion BTUs). The smaller this number, the less the industrial plant pays for delivered energy. Random samples of 11 similar plants using electricity and 16 similar plants using gas were taken, and the plant investment/quad was calculated for each. In an analysis of the difference of means of the two samples, the owners were able to reject $H _ { 0 }$ in the test $H _ { 0 } : \left( \mu _ { E } - \mu _ { G } \right) = 0$ vs. $H _ { a } : \left( \mu _ { E } - \mu _ { G } \right) > 0$ . What is our best interpretation of the result?

Consider the following set of salary data: Men (1) Women (2) Sample Size 100 80 Mean \ 12,850 \ 13,000 Standard Deviation \ 345 \ 500 To determine if women have a higher mean salary than men, we would test:

Data was collected from CEOs of companies within both the low-tech industry and the consumer products industry. The following printout compares the mean return-to-pay ratios between CEOs In the low-tech industry and CEOs in the consumer products industry. HYPOTHESIS: MEAN X = MEAN Y Using the printout above, find the test statistic necessary for testing whether the mean return-to-pay ratio of low tech CEO's exceeds the return-to-pay ratio of consumer product CEOs.

An inventor has developed a new spray coating that is designed to improve the wear of bicycle tires. To test the new coating, the inventor randomly selects one of the two tires on each of 50 Bicycles to be coated with the new spray. The bicycle is then driven for 100 miles and the amount Of the depth of the tread left on the two bicycle tires is measured (in millimeters). It is desired to Determine whether the new spray coating improves the wear of the bicycle tires. The data and Summary information is shown below: Identify the correct null and alternative hypothesis for testing whether the new spray coating improves the mean wear of the bicycle tires (which would result in a larger amount of tread left on the tire).