Question 1

Provide an appropriate response.
-Calculate the linear correlation coefficient for the data below.

Accepted Answer

A)  $0.990$ 
B)  $0.881$ 
C)  $0.819$ 
D)  $0.792$ 
A)  $0.990$ 
B)  $0.881$ 
C)  $0.819$ 
D)  $0.792$ A

Question 2

Explain the Difference between Correlation and Causation .Provide an appropriate response.
-A variable that is related to either the response variable or the predictor variable or both, but which is excluded from the analysis is a

Accepted Answer

A)  lurking variable. 
B)  random variable. 
C)  discrete variable. 
D)  qualitative variable. 
A)  lurking variable. 
B)  random variable. 
C)  discrete variable. 
D)  qualitative variable. A

Question 3

Write the word or phrase that best completes each statement or answers the question.
Provide an appropriate response.
-Construct a scatter diagram for the given data. Determine whether there is a positive linear correlation, negative linear correlation, or no linear correlation.
$\begin{array}{l|c|c|c|c|c|c|c|c|c|c|}
\mathrm{x} & -5 & -3 & 4 & 1 & -1 & -2 & 0 & 2 & 3 & -4 \
\hline \mathrm{y} & 11 & -6 & 8 & -3 & -2 & 1 & 5 & -5 & 6 & 7
\end{array}$

Accepted Answer

There appears to be no linear correlation.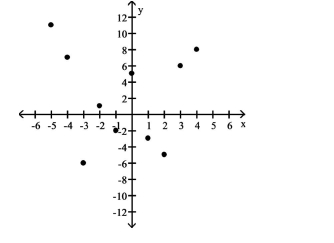

Question 4

Choose the one alternative that best completes the statement or answers the question.
-A manufacturer of boiler drums wants to use regression to predict the number of man-hours needed to erect drums in the future. The manufacturer collected a random sample of 35 boilers and measured the following two variables:
MANHRS: $y$ = Number of man-hours required to erect the drum
PRESSURE: $\mathrm { x } _ { 1 } =$ Boiler design pressure (pounds per square inch, i.e., psi)
Initially, the simple linear model $\mathrm { E } ( \mathrm { y } ) = \beta _ { 1 } + \beta _ { 1 \mathrm { x } 1 }$ was fit to the data. A printout for the analysis appears below:
UNWEIGHTED LEAST SQUARES LINEAR REGRESSION OF MANHRS
$\begin{array}{c|c|c|c|c}
\text { PREDICTOR } & & & & \
\text { VARIABLES } & \text { COEFFICIENT } & \text { STD ERROR } & \text { STUDENT'ST } & \mathrm{P} \
\hline \text { CONSTANT } & 1.88059 & 0.58380 & 3.22 & 0.0028 \
\text { PRESSURE } & 0.00321 & 0.00163 & 2.17 & 0.0300
\end{array}$

$\begin{array} { l l l l } \text { R-SQUARED } & 0.4342 & \text { RESID. MEAN SQUARE (MSE) } & 4.25460 \ \text { ADJUSTED R-SQUARED } & 0.4176 & \text { STANDARD DEVIATION } & 2.06267 \end{array}$

$\begin{array}{l|r|c|c|c|c}
\text { SOURCE } & \text { DF } & \text { SS } & \text { MS } & \mathrm{F} & \mathrm{P} \
\hline \text { REGRESSION } & 1 & 111.008 & 111.008 & 5.19 & 0.0300 \
\text { RESIDUAL } & 34 & 144.656 & 4.25160 & & \
\text { TOTAL } & 35 & 255.665 & & &
\end{array}$

Give a practical interpretation of the coefficient of determination, $\mathrm { R } ^ { 2 }$.

Accepted Answer

A)  About $43 \%$ of the sample variation in number of man-hours can be explained by the simple linear model. 
B)  $\mathrm { y } = 1.88 + 0.00321 \mathrm { x }$ will be correct $43 \%$ of the time. 
C)  Man hours needed to erect drums will be associated with boiler design pressure $43 \%$ of the time. 
D)  About $2.06 \%$ of the sample variation in number of man-hours can be explained by the simple linear model. 
A)  About $43 \%$ of the sample variation in number of man-hours can be explained by the simple linear model. 
B)  $\mathrm { y } = 1.88 + 0.00321 \mathrm { x }$ will be correct $43 \%$ of the time. 
C)  Man hours needed to erect drums will be associated with boiler design pressure $43 \%$ of the time. 
D)  About $2.06 \%$ of the sample variation in number of man-hours can be explained by the simple linear model.

Question 5

Interpret the Slope and the y-intercept of the Least-Squares Regression Line
-A real estate magazine reported the results of a regression analysis designed to predict the price (y), measured in dollars, of residential properties recently sold in a northern Virginia subdivision. One independent variable used to predict sale price is GLA, gross living area ( $x$ ), measured in square feet. Data for 157 properties were used to fit the model, $\mathrm { y } = \beta _ { 0 } + \beta _ { 1 } \mathrm { x }$. The results of the simple linear regression are provided below.
$$\hat { \mathrm { y } } = 96,600 + 22.5 \mathrm { x } \quad \mathrm { s } = 6500 \quad \mathrm { r } ^ { 2 } = - 0.77 \quad \mathrm { t } = 6.1 \text { (for testing } \beta _ { 1 } \text { ) }$$
Interpret the estimate of $\beta 0$, the $y$-intercept of the line.

Accepted Answer

A)  There is no practical interpretation, since a gross living area of 0 is a nonsensical value. 
B)  All residential properties in Virginia will sell for at least $\$ 96,600$. 
C)  About $95 \%$ of the observed sale prices fall within $\$ 96,600$ of the least squares line. 
D)  For every 1-sq ft. increase in GLA, we expect a property's sale price to increase $\$ 96,600$. 
A)  There is no practical interpretation, since a gross living area of 0 is a nonsensical value. 
B)  All residential properties in Virginia will sell for at least $\$ 96,600$. 
C)  About $95 \%$ of the observed sale prices fall within $\$ 96,600$ of the least squares line. 
D)  For every 1-sq ft. increase in GLA, we expect a property's sale price to increase $\$ 96,600$.

Question 6

Provide an appropriate response.
-The following data represent the living situation of newlyweds in a large metropolitan area and their annual household income. What percent of people who own their own home make between $\$ 35,000$ and $\$ 50,000$ per year?
$\begin{array}{l|c|c|c|c|c} 
& \$ 75,000 \
\hline \text { Own home } & 31 & 52 & 202 & 355 & 524 \
\text { Rent home } & 67 & 66 & 52 & 23 & 11 \
\text { Live w/family } & 89 & 69 & 30 & 4 & 2
\end{array}$

Accepted Answer

A)  17.4% 
B)  4.5% 
C)  30.5% 
D)  71.1% 
A)  17.4% 
B)  4.5% 
C)  30.5% 
D)  71.1%

Question 7

Perform Residual Analysis on a Regression Model
-

Accepted Answer

A)  Yes, the residuals do not display constant error variance. 
B)  Yes, there is a discernable pattern in the residuals. 
C)  No, the plot of residuals is random. 
A)  Yes, the residuals do not display constant error variance. 
B)  Yes, there is a discernable pattern in the residuals. 
C)  No, the plot of residuals is random.

Question 8

Choose the one alternative that best completes the statement or answers the question.
Use the scatter diagrams shown, labeled a through f to solve the problem.
-A scatter diagram locates a point in a two dimensional plane. The diagram locates the variable on the horizontal axis and the variable on the vertical axis.

Accepted Answer

A)  predictor; response 
B)  response; predictor 
C)  response; study 
D)  study; predictor 
A)  predictor; response 
B)  response; predictor 
C)  response; study 
D)  study; predictor

Question 9

Compute the linear correlation coefficient between the two variables and determine whether a linear relation exists.
-The table shows the number of days off last year and the earnings for the year (in thousands of dollars) for nine randomly selected insurance salesmen.

Accepted Answer

A)  $\mathrm { r } = - 0.991$; linear relation exists 
B)  $\mathrm { r } = - 0.991$; no linear relation exists 
C)  $\mathrm { r } = - 0.899$; linear relation exists 
D)  $\mathrm { r } = - 0.899$; no linear relation exists 
A)  $\mathrm { r } = - 0.991$; linear relation exists 
B)  $\mathrm { r } = - 0.991$; no linear relation exists 
C)  $\mathrm { r } = - 0.899$; linear relation exists 
D)  $\mathrm { r } = - 0.899$; no linear relation exists

Question 10

Compute the linear correlation coefficient between the two variables and determine whether a linear relation exists.
-To investigate the relationship between yield of soybeans and the amount of fertilizer used, a researcher divides a field into eight plots of equal size and applies a different amount of fertilizer to each plot. The table shows the yield of soybeans and the amount of fertilizer used for each plot.
$\begin{array}{c|cccccccc}
\text { Amount of fertilizer (pounds), } & 1 & 1.5 & 2 & 2.5 & 3 & 3.5 & 4 & 4.5 \
\hline \text { Yield of soybeans (pounds), y } & 25 & 21 & 27 & 28 & 36 & 35 & 32 & 34
\end{array}$

Accepted Answer

A)  $r = 0.819$; linear relation exists 
B)  $\mathrm { r } = 0.729$; no linear relation exists 
C)  $r = 0.683$; linear relation exists 
D)  $\mathrm { r } = 0.683$; no linear relation exists 
A)  $r = 0.819$; linear relation exists 
B)  $\mathrm { r } = 0.729$; no linear relation exists 
C)  $r = 0.683$; linear relation exists 
D)  $\mathrm { r } = 0.683$; no linear relation exists

Question 11

Compute the linear correlation coefficient between the two variables and determine whether a linear relation exists.
-A manager wishes to determine whether there is a relationship between the number of years her sales representatives have been with the company and their average monthly sales. The table shows the years of service for each of her sales representatives and their average monthly sales (in thousands of dollars).
$\begin{array}{l|c|c|c|c|c|c|c|c|c}
\text { Years with company, } x & 4 & 5 & 12 & 9 & 10 & 17 & 5 & 3 & 13 \
\hline \text { Sales, } y & 21 & 23 & 68 & 52 & 55 & 51 & 38 & 45 & 110
\end{array}$

Accepted Answer

A)  $r = 0.632$; no linear relation exists 
B)  $\mathrm { r } = 0.632$; linear relation exists 
C)  $\mathrm { r } = 0.717$; linear relation exists 
D)  $\mathrm { r } = 0.717$; no linear relation exists 
A)  $r = 0.632$; no linear relation exists 
B)  $\mathrm { r } = 0.632$; linear relation exists 
C)  $\mathrm { r } = 0.717$; linear relation exists 
D)  $\mathrm { r } = 0.717$; no linear relation exists

Question 12

Choose the one alternative that best completes the statement or answers the question.
-Civil engineers often use the straight-line equation, $\mathrm { E } ( \mathrm { y } ) = \beta _ { 0 } + \beta _ { 1 } \mathrm { x }$, to model the relationship between the mean shear strength $\mathrm { E } ( \mathrm { y } )$ of masonry joints and precompression stress, $x$. To test this theory, a series of stress tests were performed on solid bricks arranged in triplets and joined with mortar. The precompression stress was varied for each triplet and the ultimate shear load just before failure (called the shear strength) was recorded. The stress results for $\mathrm { n } = 7$ triplet tests is shown in the accompanying table followed by a SAS printout of the regression analysis.
$\begin{array}{l|ccccccc}
\text { Triplet Test } & 1 & 2 & 3 & 4 & 5 & 6 & 7 \
\hline \text { Shear Strength (tons), } \mathrm{y} & 1.00 & 2.18 & 2.24 & 2.41 & 2.59 & 2.82 & 3.06 \
\hline \text { Precomp. Stress (tons), } \mathrm{x} & 0 & 0.60 & 1.20 & 1.33 & 1.43 & 1.75 & 1.75
\end{array}$

$\text { Analysis of Variance }$

$\begin{array}{lccccc} 
& {\text { Sum of }} & \text { Mean } \
\text { Source } & \text { DF } & \text { Squares } & \text { Square } & \text { F Value } & \text { Prob > F } \
\text { Model } & 1 & 2.39555 & 2.39555 & 47.732 & 0.0010 \
\text { Error } & 5 & 0.25094 & 0.05019 & & \
\text { C Total } & 6 & 2.64649 & & &
\end{array}$

$\begin{array}{llll}
\text { Root MSE } & 0.22403 & \text { R-square } & 0.9052 \
\text { Dep Mean } & 2.32857 & \text { Adj R-sq } & 0.8862 \
\text { C.V. } & 9.62073 & &
\end{array}$

$\begin{array}{l}
\text { Parameter Estimates }\
\begin{array}{llllll} 
& & \text { Parameter } & \text { Standard } & \text { T for HO: } & \
\text { Variable } & \text { DF } & \text { Estimate } & \text { Error } & \text { Parameter }=0 & \text { Prob }>|\mathrm{T}| \
\text { INTERCEP } & 1 & 1.191930 & 0.18503093 & 6.442 & 0.0013 \
\mathrm{X} & 1 & 0.987157 & 0.14288331 & 6.909 & 0.0010
\end{array}
\end{array}$

Give a practical interpretation of $R ^ { 2 }$, the coefficient of determination for the least squares model.

Accepted Answer

A)  About $91 \%$ of the total variation in the sample of $y$-values can be explained by (or attributed to) the linear relationship between shear strength and precompression stress. 
B)  In repeated sampling, approximately $91 \%$ of all similarly constructed regression lines will accurately predict shear strength. 
C)  We expect to predict the shear strength of a triplet test to within about 91 ton of its true value. 
D)  We expect about $91 \%$ of the observed shear strength values to lie on the least squares line. 
A)  About $91 \%$ of the total variation in the sample of $y$-values can be explained by (or attributed to) the linear relationship between shear strength and precompression stress. 
B)  In repeated sampling, approximately $91 \%$ of all similarly constructed regression lines will accurately predict shear strength. 
C)  We expect to predict the shear strength of a triplet test to within about 91 ton of its true value. 
D)  We expect about $91 \%$ of the observed shear strength values to lie on the least squares line.

Question 13

Write the word or phrase that best completes each statement or answers the question.
Construct a scatter diagram for the data.
-The data below are the number of absences and the final grades of 9 randomly selected students from a literature class.
$\begin{array}{|l|c|c|c|c|c|c|c|c|c|}
\text { Number of absences, } x & 0 & 3 & 6 & 4 & 9 & 2 & 15 & 8 & 5 \
\hline \text { Final grade, } y & 98 & 86 & 80 & 82 & 71 & 92 & 55 & 76 & 82
\end{array}$

Accepted Answer

The answer of Write the word or phrase that best...

Question 14

Choose the one alternative that best completes the statement or answers the question.
-In an area of Russia, records were kept on the relationship between the rainfall (in inches) and the yield of wheat (bushels per acre). The data for a 9 year period is as follows:
$\begin{array}{l|ccccccccc}
\text { Rain Fall, x } & 13.1 & 11.4 & 16.0 & 15.1 & 21.4 & 12.9 & 9.6 & 18.2 & 18.6 \
\hline \text { Yield, y } & 48.5 & 44.2 & 56.8 & 80.4 & 47.2 & 29.9 & 74.0 & 74.0 & 76.8
\end{array}$

The equation of the line of least squares is given as $\mathrm { y } = - 9.12 + 4.38 \mathrm { x }$. What would be the expected number of inches of rain if the yield is 60 bushels of wheat per acre?

Accepted Answer

A)  $15.78$ 
B)  $253.68$ 
C)  $11.62$ 
D)  $64.74$ 
A)  $15.78$ 
B)  $253.68$ 
C)  $11.62$ 
D)  $64.74$

Question 15

Interpret the Slope and the y-intercept of the Least-Squares Regression Line
-Is there a relationship between the raises administrators at State University receive and their performance on the job? A faculty group wants to determine whether job rating (x) is a useful linear predictor of raise (y). Consequently, the group considered the straight-line regression model, $\hat { y } = \beta _ { 0 } + \beta _ { 1 } x$. Using the method of least squares, the faculty group obtained the following prediction equation, $\mathrm { y } = 14,000 + 2,000 \mathrm { x }$. Interpret the estimated slope of the line.

Accepted Answer

A)  For a 1-point increase in an administrator's rating, we estimate the administrator's raise to increase $\$ 2,000$. 
B)  For a 1-point increase in an administrator's rating, we estimate the administrator's raise to decrease $\$ 2,000$. 
C)  For an administrator with a rating of $1.0$, we estimate his/her raise to be $\$ 2,000$. 
D)  For a $\$ 1$ increase in an administrator's raise, we estimate the administrator's rating to decrease 2,000 points. 
A)  For a 1-point increase in an administrator's rating, we estimate the administrator's raise to increase $\$ 2,000$. 
B)  For a 1-point increase in an administrator's rating, we estimate the administrator's raise to decrease $\$ 2,000$. 
C)  For an administrator with a rating of $1.0$, we estimate his/her raise to be $\$ 2,000$. 
D)  For a $\$ 1$ increase in an administrator's raise, we estimate the administrator's rating to decrease 2,000 points.

Question 16

A scatter diagram is given with one of the points labeled ʺA.ʺ In addition, there are two least -squares regression lines
drawn. The solid line excludes the point A. The dashed line includes the point A. Based on the graph, is the point A
influential
-What effect will an influential observation have upon the graph of the least squares regression line

Accepted Answer

A)  It will pull the graph toward the observation. 
B)  It will have no effect. 
C)  It will push the graph away from the observation. 
D)  It will lower the value of the correlation coefficient to make further analysis meaningless. 
A)  It will pull the graph toward the observation. 
B)  It will have no effect. 
C)  It will push the graph away from the observation. 
D)  It will lower the value of the correlation coefficient to make further analysis meaningless.

Question 17

Change the exponential expression to an equivalent expression involving a logarithm.
-$$4 ^ { 3 } = x$$

Accepted Answer

A)  $\log _ { 4 } x = 3$ 
B)  $\log _ { \mathrm { x } } 4 = 3$ 
C)  $\log _ { 3 } x = 4$ 
D)  $\log _ { 4 } 3 = x$ 
A)  $\log _ { 4 } x = 3$ 
B)  $\log _ { \mathrm { x } } 4 = 3$ 
C)  $\log _ { 3 } x = 4$ 
D)  $\log _ { 4 } 3 = x$

Question 18

Choose the one alternative that best completes the statement or answers the question.
-The coefficient of determination is the of the linear correlation coefficient.

Accepted Answer

A)  square 
B)  square root 
C)  opposite 
D)  reciprocal 
A)  square 
B)  square root 
C)  opposite 
D)  reciprocal

Question 19

Choose the one alternative that best completes the statement or answers the question.
-The measures the percentage of total variation in the response variable that is explained by the least squares regression line.

Accepted Answer

A)  coefficient of determination 
B)  coefficient of linear correlation 
C)  sum of the residuals squared 
D)  slope of the regression line 
A)  coefficient of determination 
B)  coefficient of linear correlation 
C)  sum of the residuals squared 
D)  slope of the regression line

Question 20

Compute the Sum of Squared Residuals
-The regression line for the given data is $\mathrm { y } = 5.044 \mathrm { x } + 56.11$. Determine the residual of a data point for which $x =$ 8 and $y = 88$.
$\begin{array}{l|c|c|c|c|c|c|c|c|c|c|}
\text { Hours, } \mathrm{x} & 3 & 5 & 2 & 8 & 2 & 4 & 4 & 5 & 6 & 3 \
\hline \text { Scores, } \mathrm{y} & 65 & 80 & 60 & 88 & 66 & 78 & 85 & 90 & 90 & 71
\end{array}$

Accepted Answer

A)  $- 8.462$ 
B)  $184.462$ 
C)  $96.462$ 
D)  $- 491.982$ 
A)  $- 8.462$ 
B)  $184.462$ 
C)  $96.462$ 
D)  $- 491.982$

Provide an appropriate response. -Calculate the linear correlation coefficient for the data below.

Explain the Difference between Correlation and Causation .Provide an appropriate response. -A variable that is related to either the response variable or the predictor variable or both, but which is excluded from the analysis is a

Perform Residual Analysis on a Regression Model -

Compute the linear correlation coefficient between the two variables and determine whether a linear relation exists. -The table shows the number of days off last year and the earnings for the year (in thousands of dollars) for nine randomly selected insurance salesmen.

Change the exponential expression to an equivalent expression involving a logarithm. - $4 ^ { 3 } = x$

Choose the one alternative that best completes the statement or answers the question. -The coefficient of determination is the of the linear correlation coefficient.

Choose the one alternative that best completes the statement or answers the question. -The measures the percentage of total variation in the response variable that is explained by the least squares regression line.

Compute the Sum of Squared Residuals -The regression line for the given data is $\mathrm { y } = 5.044 \mathrm { x } + 56.11$ . Determine the residual of a data point for which $x =$ 8 and $y = 88$ . Hours, 3 5 2 8 2 4 4 5 6 3 Scores, 65 80 60 88 66 78 85 90 90 71

Data Collection

Creating Tables and Drawing Pictures of Data

Numerically Summarizing Data

Probability

Discrete Probability Distributions

The Normal Probability Distribution

Sampling Distributions

Estimating the Value of a Parameter Using Confidence Intervals

Hypothesis Tests Regarding a Parameter

Inference on Two Samples

Inference on Categorical Data

Comparing Three or More Means

Inference of the Least-Squares Regression Model and Multiple Regression

Nonparametric Statistics

Filters

Exam 4: Describing the Relation Between Two Variables