Exam 8: Sequences, Series, and Probability
Exam 1: Functions and Their Graphs120 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions120 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability118 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus120 Questions
Select questions type
Use mathematical induction to prove the following for every positive integer .
(Essay)
4.9/5  (44)
(44)
Determine the sample space for the experiment.
Two marbles are selected from marbles labeled A through where the marbles are not replaced and the order of selection does not matter.
(Multiple Choice)
4.9/5  (26)
(26)
Write an expression for the apparent th term of the sequence. (Assume that begins with 1.)
(Multiple Choice)
4.7/5  (38)
(38)
Find the indicated th term of the geometric sequence.
4th term:
(Multiple Choice)
4.8/5  (34)
(34)
The first two terms of the arithmetic sequence are given. Find the indicated term.
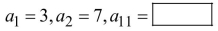
(Multiple Choice)
5.0/5  (39)
(39)
Use mathematical induction to prove the following for every positive integer .
(Essay)
4.7/5  (32)
(32)
Find the number of distinguishable permutations of the group of letters.
(Multiple Choice)
4.9/5  (35)
(35)
Use the Binomial Theorem to expand the complex number. Simplify your result.
(Multiple Choice)
4.9/5  (39)
(39)
You are given the probability that an event will not happen. Find the probability that the event will happen.
(Multiple Choice)
4.9/5  (38)
(38)
Find the probability for the experiment of tossing a coin four times and getting at least two heads. Use the sample space
Sequals HHHH HHHT HHTH HTHH THHH HHTT HTHT THHT THTH HTTH TTHH TTTH TTHT THTT HTTT TTTT
(Multiple Choice)
4.9/5  (31)
(31)
Use the Binomial Theorem to expand and simplify the expression.
(Multiple Choice)
4.9/5  (44)
(44)
Use mathematical induction to prove the following for every positive integer .
(Essay)
4.8/5  (44)
(44)
Determine whether the sequence is geometric. If so, find the common ratio.
(Multiple Choice)
4.8/5  (38)
(38)
You are given the probability that an event will happen. Find the probability that the event will not happen.
(Multiple Choice)
4.8/5  (45)
(45)
Showing 41 - 60 of 118
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)