Exam 5: A: Induction and Recursion

give a recursive definition with initial condition(s). -The Fibonacci numbers 1, 1, 2, 3, 5, 8, 13, . . .

Use mathematical induction to prove that $1 + 3 + 9 + 27 + \cdots + 3 ^ { n } = \frac { 3 ^ { n + 1 } - 1 } { 2 } \text { for all } n \geq 0 \text {. }$

give a recursive definition with initial condition(s) of the set S . -The set of strings 1, 111, 11111, 1111111, . . .

give a recursive definition with initial condition(s). -The set {1, 1/3, 1/9, 1/27, . . .}

Suppose that the only paper money consists of 3-dollar bills and 10-dollar bills. Show that any dollar amount greater than 17 dollars could be made from a combination of these bills.

Consider the following program segment: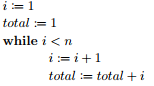 Let p be the proposition $" \text { total } = \frac { i ( i + 1 ) } { 2 } \text { and } i \leq n . "$ Use mathematical induction to prove that p is a loop invariant.

give a recursive definition with initial condition(s) of the set S . -{3, 7, 11, 15, 19, 23, . . .}

give a recursive definition with initial condition(s) of the set S . -All positive integer multiples of 5

A T -omino is a tile pictured at the right. Prove that every $2 ^ { n } \times 2 ^ { n } ( n > 1 )$ chessboard can be tiled with T-ominoes.

Find f(2) and f(3) if f(n) = f(n − 1)/f(n − 2), f(0) = 2, f(1) = 5.

Suppose you wish to prove that the following is true for all positive integers n by using mathematical induction: 1+3+5+...+(2 n-1)=n² (a) Write P(1). (b) Write P(72). (c) Write P(73). (d) Use P(72) to prove P(73). (e) Write P(k). (f) Write P(k + 1). (g) Use mathematical induction to prove that P(n) is true for all positive integers n.

Use mathematical induction to prove that $2 n + 3 \leq 2 ^ { n } \text { for all } n \geq 4$

Floor borders one foot wide and of varying lengths are to be covered with nonoverlapping tiles that are available in two sizes: $1 ^ { \prime } \times 3 ^ { \prime }$ and $1 ^ { \prime } \times 5 ^ { \prime }$ sizes. Assuming that the supply of each size is infinite, prove that every $1 ^ { \prime } \times n ^ { \prime }$ border $( n > 7 )$ can be covered with these tiles.

Use mathematical induction to prove that $3 \mid \left( n ^ { 3 } + 3 n ^ { 2 } + 2 n \right) \text { for all } n \geq 1$

Use mathematical induction to prove that $n ^ { 3 } > n ^ { 2 } + 3 \text { for all } n \geq 2$

Prove that $\sum _ { j = n } ^ { 2 n - 1 } ( 2 j + 1 ) = 3 n ^ { 2 } \text { for all positive integers } n$

Find $f ( 2 )$ and $f ( 3 )$ if $f ( n ) = 2 f ( n - 1 ) + 6 , f ( 0 ) = 3$

give a recursive definition with initial condition(s). -The set {. . . , −4, −2, 0, 2, 4, 6, . . .}

give a recursive definition with initial condition(s). -The sequence $a _ { 1 } = 16 , a _ { 2 } = 13 , a _ { 3 } = 10 , a _ { 4 } = 7 , \ldots$

give a recursive definition (with initial condition(s)) of $\left\{ a _ { n } \right\} \quad ( n = 1,2,3 , \ldots )$ - $a _ { n } = n ^ { 2 } + n$