Exam 5: A: Induction and Recursion
Exam 1: The Foundations: Logic and Proofs18 Questions
Exam 1: A: the Foundations: Logic and Proofs201 Questions
Exam 2: Basic Structures: Sets, Functions, Sequences, Sums, Matrices5 Questions
Exam 2: A: Basic Structures: Sets, Functions, Sequences, Sums, Matrices210 Questions
Exam 3: Algorithms8 Questions
Exam 3: A: Algorithms54 Questions
Exam 4: Number Theory and Cryptography10 Questions
Exam 4: A: Number Theory and Cryptography149 Questions
Exam 5: Induction and Recursion10 Questions
Exam 5: A: Induction and Recursion51 Questions
Exam 6: Counting14 Questions
Exam 6: A: Counting155 Questions
Exam 7: Discrete Probability9 Questions
Exam 7: A: Discrete Probability50 Questions
Exam 8: Advanced Counting Techniques16 Questions
Exam 8: A: Advanced Counting Techniques124 Questions
Exam 9: Relations13 Questions
Exam 9: A: Relations72 Questions
Exam 10: Graphs14 Questions
Exam 10: A: Graphs131 Questions
Exam 11: Trees13 Questions
Exam 11: A: Trees94 Questions
Exam 12: Boolean Algebra11 Questions
Exam 12: A: Boolean Algebra67 Questions
Exam 13: Modeling Computation14 Questions
Exam 13: A: Modeling Computation67 Questions
Exam 14: Mathematics Problem Set: Set Theory, Number Theory, Combinatorics, and Boolean Algebra29 Questions
Select questions type
Verify that the following program segment is correct with respect to the initial assertion T and the final
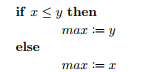
(Essay)
4.8/5  (35)
(35)
Let S be the set of positive integers defined by:
Basis step: 4 S .
Recursive step: If n S , then and
(a) Show that if , then (mod 6).
(b) Show that there exists an integer (mod 6) that does not belong to
(Essay)
4.9/5  (34)
(34)
give a recursive definition with initial condition(s).
-The set {1, 5, 9, 13, 17, . . .}
(Short Answer)
4.8/5  (35)
(35)
give a recursive definition with initial condition(s).
-The set {0, 3, 6, 9, . . .}
(Short Answer)
4.9/5  (24)
(24)
Use mathematical induction to prove that every integer amount of postage of six cents or more can be formed using 3-cent and 4-cent stamps.
(Essay)
4.9/5  (31)
(31)
Showing 41 - 51 of 51
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)