Exam 3: Vectors
Exam 1: Physics and Measurement25 Questions
Exam 2: Motion in One Dimension66 Questions
Exam 3: Vectors47 Questions
Exam 4: Motion in Two Dimensions79 Questions
Exam 5: The Laws of Motion113 Questions
Exam 6: Circular Motion and Other Applications of Newtons Laws55 Questions
Exam 7: Energy of a System74 Questions
Exam 8: Conservation of Energy84 Questions
Exam 9: Linear Momentum and Collisions89 Questions
Exam 10: Rotation of a Rigid Object About a Fixed Axis82 Questions
Exam 11: Angular Momentum46 Questions
Exam 12: Static Equilibrium and Elasticity34 Questions
Exam 13: Universal Gravitation47 Questions
Exam 14: Fluid Mechanics53 Questions
Exam 15: Oscillatory Motion41 Questions
Exam 16: Wave Motion82 Questions
Exam 18: Superposition and Standing Waves72 Questions
Exam 19: Temperature47 Questions
Exam 20: The First Law of Thermodynamics61 Questions
Exam 21: The Kinetic Theory of Gases38 Questions
Exam 22: Heat Engines, Entropy, and the Second Law of Thermodynamics55 Questions
Exam 23: Electric Fields67 Questions
Exam 24: Gausss Law82 Questions
Exam 25: Electric Potential111 Questions
Exam 26: Capacitance and Dielectrics63 Questions
Exam 27: Current and Resistance34 Questions
Exam 28: Direct-Current Circuits84 Questions
Exam 29: Magnetic Fields80 Questions
Exam 30: Sources of the Magnetic Field95 Questions
Exam 31: Faradays Law62 Questions
Exam 32: Inductance23 Questions
Exam 33: Alternating-Current Circuits65 Questions
Exam 34: Electromagnetic Waves40 Questions
Exam 35: The Nature of Light and the Principles of Ray Optics37 Questions
Exam 36: Image Formation43 Questions
Exam 37: Wave Optics48 Questions
Exam 38: Diffraction Patterns and Polarization47 Questions
Exam 39: Relativity34 Questions
Exam 40: Introduction to Quantum Physics48 Questions
Exam 41: Quantum Mechanics33 Questions
Exam 42: Atomic Physics59 Questions
Exam 43: Molecules and Solids46 Questions
Exam 44: Nuclear Structure89 Questions
Exam 46: Particle Physics and Cosmology34 Questions
Select questions type
When vector 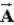 is added to vector
is added to vector  , which has a magnitude of 5.0, the vector representing their sum is perpendicular to
, which has a magnitude of 5.0, the vector representing their sum is perpendicular to 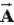 and has a magnitude that is twice that of
and has a magnitude that is twice that of 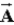 . What is the magnitude of
. What is the magnitude of 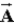 ?
?
(Multiple Choice)
4.9/5  (35)
(35)
When three vectors, 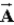 ,
,  , and
, and 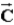 are placed head to tail, the vector sum
are placed head to tail, the vector sum 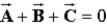 . If the vectors all have the same magnitude, the angle between the directions of any two adjacent vectors is
. If the vectors all have the same magnitude, the angle between the directions of any two adjacent vectors is
(Multiple Choice)
4.9/5  (37)
(37)
A vector starts at coordinate (3.0, 4.0) and ends at coordinate (−2.0, 16.0). What are the magnitude and direction of this vector?
(Short Answer)
4.8/5  (38)
(38)
If vector 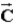 is added to vector
is added to vector  , the result is
, the result is 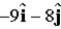 . If
. If  is subtracted from
is subtracted from 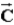 , the result is
, the result is 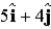 . What is the direction of
. What is the direction of  (to the nearest degree)?
(to the nearest degree)?
(Multiple Choice)
4.7/5  (33)
(33)
Starting from one oasis, a camel walks 25 km in a direction 30° south of west and then walks 30 km toward the north to a second oasis. What distance separates the two oases?
(Multiple Choice)
4.9/5  (35)
(35)
Instructions: On occasion, the notation ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-3. Which diagram below correctly represents ?](https://storage.examlex.com/TB8245/11eb6adc_edad_c64b_b0cf_0bd162eea8eb_TB8245_11.jpg) = [A, θ] will be a shorthand notation for
= [A, θ] will be a shorthand notation for ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-3. Which diagram below correctly represents ?](https://storage.examlex.com/TB8245/11eb6adc_edad_ed5c_b0cf_abaa9c299801_TB8245_11.jpg) .
Exhibit 3-3
The vectors
.
Exhibit 3-3
The vectors ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-3. Which diagram below correctly represents ?](https://storage.examlex.com/TB8245/11eb6adc_edad_ed5d_b0cf_5d66546fbc87_TB8245_11.jpg) ,
, ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-3. Which diagram below correctly represents ?](https://storage.examlex.com/TB8245/11eb6adc_edad_ed5e_b0cf_7f27db1f841f_TB8245_11.jpg) , and
, and ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-3. Which diagram below correctly represents ?](https://storage.examlex.com/TB8245/11eb6adc_edae_146f_b0cf_fba56094bc35_TB8245_11.jpg) are shown below.
are shown below. ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-3. Which diagram below correctly represents ?](https://storage.examlex.com/TB8245/11eb6adc_edae_1470_b0cf_ad4d18d0fb5d_TB8245_00.jpg) Use this exhibit to answer the following question(s).
-Refer to Exhibit 3-3. Which diagram below correctly represents
Use this exhibit to answer the following question(s).
-Refer to Exhibit 3-3. Which diagram below correctly represents ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-3. Which diagram below correctly represents ?](https://storage.examlex.com/TB8245/11eb6adc_edae_3b81_b0cf_45af095442d6_TB8245_00.jpg) ?
?
(Multiple Choice)
4.9/5  (45)
(45)
A vector,  , when added to the vector
, when added to the vector 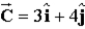 yields a resultant vector which is in the positive y direction and has a magnitude equal to that of
yields a resultant vector which is in the positive y direction and has a magnitude equal to that of 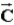 . What is the magnitude of
. What is the magnitude of  ?
?
(Multiple Choice)
4.7/5  (36)
(36)
If ![If = [2.5 cm, 80°], i.e., the magnitude and direction of are 2.5 cm and 80°, = [3.5 cm, 120°], and , what is the direction of (to the nearest degree)?](https://storage.examlex.com/TB8245/11eb6adc_eda4_9e21_b0cf_f105b290aac4_TB8245_11.jpg) = [2.5 cm, 80°], i.e., the magnitude and direction of
= [2.5 cm, 80°], i.e., the magnitude and direction of ![If = [2.5 cm, 80°], i.e., the magnitude and direction of are 2.5 cm and 80°, = [3.5 cm, 120°], and , what is the direction of (to the nearest degree)?](https://storage.examlex.com/TB8245/11eb6adc_eda4_9e22_b0cf_d15e66c8b49f_TB8245_11.jpg) are 2.5 cm and 80°,
are 2.5 cm and 80°, ![If = [2.5 cm, 80°], i.e., the magnitude and direction of are 2.5 cm and 80°, = [3.5 cm, 120°], and , what is the direction of (to the nearest degree)?](https://storage.examlex.com/TB8245/11eb6adc_eda4_9e23_b0cf_5f914dc9282e_TB8245_11.jpg) = [3.5 cm, 120°], and
= [3.5 cm, 120°], and ![If = [2.5 cm, 80°], i.e., the magnitude and direction of are 2.5 cm and 80°, = [3.5 cm, 120°], and , what is the direction of (to the nearest degree)?](https://storage.examlex.com/TB8245/11eb6adc_eda4_c534_b0cf_e30d1fc98f97_TB8245_11.jpg) , what is the direction of
, what is the direction of ![If = [2.5 cm, 80°], i.e., the magnitude and direction of are 2.5 cm and 80°, = [3.5 cm, 120°], and , what is the direction of (to the nearest degree)?](https://storage.examlex.com/TB8245/11eb6adc_eda4_c535_b0cf_67b7d01e6189_TB8245_11.jpg) (to the nearest degree)?
(to the nearest degree)?
(Multiple Choice)
4.8/5  (28)
(28)
Instructions: On occasion, the notation ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-4. The total displacement of the sailboat, the vector sum of its displacements OB, BC, CD and DE, is](https://storage.examlex.com/TB8245/11eb6adc_edad_c64b_b0cf_0bd162eea8eb_TB8245_11.jpg) = [A, θ] will be a shorthand notation for
= [A, θ] will be a shorthand notation for ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-4. The total displacement of the sailboat, the vector sum of its displacements OB, BC, CD and DE, is](https://storage.examlex.com/TB8245/11eb6adc_edad_ed5c_b0cf_abaa9c299801_TB8245_11.jpg) .
Exhibit 3-3
The vectors
.
Exhibit 3-3
The vectors ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-4. The total displacement of the sailboat, the vector sum of its displacements OB, BC, CD and DE, is](https://storage.examlex.com/TB8245/11eb6adc_edad_ed5d_b0cf_5d66546fbc87_TB8245_11.jpg) ,
, ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-4. The total displacement of the sailboat, the vector sum of its displacements OB, BC, CD and DE, is](https://storage.examlex.com/TB8245/11eb6adc_edad_ed5e_b0cf_7f27db1f841f_TB8245_11.jpg) , and
, and ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-4. The total displacement of the sailboat, the vector sum of its displacements OB, BC, CD and DE, is](https://storage.examlex.com/TB8245/11eb6adc_edae_146f_b0cf_fba56094bc35_TB8245_11.jpg) are shown below.
are shown below. ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-4. The total displacement of the sailboat, the vector sum of its displacements OB, BC, CD and DE, is](https://storage.examlex.com/TB8245/11eb6adc_edae_1470_b0cf_ad4d18d0fb5d_TB8245_00.jpg) Use this exhibit to answer the following question(s).
-Refer to Exhibit 3-4. The total displacement of the sailboat, the vector sum of its displacements OB, BC, CD and DE, is
Use this exhibit to answer the following question(s).
-Refer to Exhibit 3-4. The total displacement of the sailboat, the vector sum of its displacements OB, BC, CD and DE, is
(Multiple Choice)
4.8/5  (28)
(28)
Instructions: On occasion, the notation ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-1 The three forces shown act on a particle. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-1. What is the magnitude of the resultant of these three forces?](https://storage.examlex.com/TB8245/11eb6adc_eda7_ab84_b0cf_fdb0f28951f8_TB8245_11.jpg) = [A, θ] will be a shorthand notation for
= [A, θ] will be a shorthand notation for ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-1 The three forces shown act on a particle. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-1. What is the magnitude of the resultant of these three forces?](https://storage.examlex.com/TB8245/11eb6adc_eda7_ab85_b0cf_13480d1365d6_TB8245_11.jpg) .
Exhibit 3-1
The three forces shown act on a particle.
.
Exhibit 3-1
The three forces shown act on a particle. ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-1 The three forces shown act on a particle. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-1. What is the magnitude of the resultant of these three forces?](https://storage.examlex.com/TB8245/11eb6adc_eda7_ab86_b0cf_030e3d0c9ee4_TB8245_00.jpg) Use this exhibit to answer the following question(s).
-Refer to Exhibit 3-1. What is the magnitude of the resultant of these three forces?
Use this exhibit to answer the following question(s).
-Refer to Exhibit 3-1. What is the magnitude of the resultant of these three forces?
(Multiple Choice)
4.8/5  (29)
(29)
Adding vectors 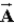 and
and  by the graphical method gives the same result for
by the graphical method gives the same result for 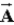 +
+  and
and  +
+ 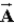 . If both additions are done graphically from the same origin, the resultant is the vector that goes from the tail of the first vector to the tip of the second vector, i.e, it is represented by a diagonal of the parallelogram formed by showing both additions in the same figure. Note that a parallelogram has 2 diagonals. Keara says that the sum of two vectors by the parallelogram method is
. If both additions are done graphically from the same origin, the resultant is the vector that goes from the tail of the first vector to the tip of the second vector, i.e, it is represented by a diagonal of the parallelogram formed by showing both additions in the same figure. Note that a parallelogram has 2 diagonals. Keara says that the sum of two vectors by the parallelogram method is 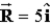 . Shamu says it is
. Shamu says it is 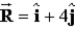 . Both used the parallelogram method, but one used the wrong diagonal. Which one of the vector pairs below contains the original two vectors?
. Both used the parallelogram method, but one used the wrong diagonal. Which one of the vector pairs below contains the original two vectors?
(Multiple Choice)
4.8/5  (34)
(34)
Instructions: On occasion, the notation ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . -A student decides to spend spring break by driving 50 miles due east, then 50 miles 30 degrees south of east, then 50 miles 30 degrees south of that direction, and to continue to drive 50 miles deviating by 30 degrees each time until he returns to his original position. How far will he drive, and how many vectors must he sum to calculate his displacement?](https://storage.examlex.com/TB8245/11eb6adc_eda9_5947_b0cf_9b90518a115d_TB8245_11.jpg) = [A, θ] will be a shorthand notation for
= [A, θ] will be a shorthand notation for ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . -A student decides to spend spring break by driving 50 miles due east, then 50 miles 30 degrees south of east, then 50 miles 30 degrees south of that direction, and to continue to drive 50 miles deviating by 30 degrees each time until he returns to his original position. How far will he drive, and how many vectors must he sum to calculate his displacement?](https://storage.examlex.com/TB8245/11eb6adc_eda9_5948_b0cf_97f3c61c9a30_TB8245_11.jpg) .
-A student decides to spend spring break by driving 50 miles due east, then 50 miles 30 degrees south of east, then 50 miles 30 degrees south of that direction, and to continue to drive 50 miles deviating by 30 degrees each time until he returns to his original position. How far will he drive, and how many vectors must he sum to calculate his displacement?
.
-A student decides to spend spring break by driving 50 miles due east, then 50 miles 30 degrees south of east, then 50 miles 30 degrees south of that direction, and to continue to drive 50 miles deviating by 30 degrees each time until he returns to his original position. How far will he drive, and how many vectors must he sum to calculate his displacement?
(Multiple Choice)
4.9/5  (35)
(35)
Instructions: On occasion, the notation ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-4. The total distance it travels is](https://storage.examlex.com/TB8245/11eb6adc_edad_c64b_b0cf_0bd162eea8eb_TB8245_11.jpg) = [A, θ] will be a shorthand notation for
= [A, θ] will be a shorthand notation for ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-4. The total distance it travels is](https://storage.examlex.com/TB8245/11eb6adc_edad_ed5c_b0cf_abaa9c299801_TB8245_11.jpg) .
Exhibit 3-3
The vectors
.
Exhibit 3-3
The vectors ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-4. The total distance it travels is](https://storage.examlex.com/TB8245/11eb6adc_edad_ed5d_b0cf_5d66546fbc87_TB8245_11.jpg) ,
, ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-4. The total distance it travels is](https://storage.examlex.com/TB8245/11eb6adc_edad_ed5e_b0cf_7f27db1f841f_TB8245_11.jpg) , and
, and ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-4. The total distance it travels is](https://storage.examlex.com/TB8245/11eb6adc_edae_146f_b0cf_fba56094bc35_TB8245_11.jpg) are shown below.
are shown below. ![Instructions: On occasion, the notation = [A, θ] will be a shorthand notation for . Exhibit 3-3 The vectors , , and are shown below. Use this exhibit to answer the following question(s). -Refer to Exhibit 3-4. The total distance it travels is](https://storage.examlex.com/TB8245/11eb6adc_edae_1470_b0cf_ad4d18d0fb5d_TB8245_00.jpg) Use this exhibit to answer the following question(s).
-Refer to Exhibit 3-4. The total distance it travels is
Use this exhibit to answer the following question(s).
-Refer to Exhibit 3-4. The total distance it travels is
(Multiple Choice)
4.9/5  (36)
(36)
Given two non-zero vectors, 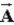 and
and  , such that
, such that 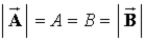 , the sum
, the sum 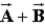 satisfies
satisfies
(Multiple Choice)
4.8/5  (40)
(40)
If ![If = [10 m, 30°] and = [25 m, 130°], what is the magnitude of the sum of these two vectors?](https://storage.examlex.com/TB8245/11eb6adc_eda3_3e82_b0cf_cd4d06451e1c_TB8245_11.jpg) = [10 m, 30°] and
= [10 m, 30°] and ![If = [10 m, 30°] and = [25 m, 130°], what is the magnitude of the sum of these two vectors?](https://storage.examlex.com/TB8245/11eb6adc_eda3_3e83_b0cf_73ee89fc3817_TB8245_11.jpg) = [25 m, 130°], what is the magnitude of the sum of these two vectors?
= [25 m, 130°], what is the magnitude of the sum of these two vectors?
(Multiple Choice)
4.8/5  (28)
(28)
Showing 21 - 40 of 47
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)