Exam 21: Supplement D Linear Programming
Exam 1: Using Operations to Create Value115 Questions
Exam 2: Process Strategy and Analysis239 Questions
Exam 3: Quality and Performance198 Questions
Exam 4: Capacity Planning120 Questions
Exam 5: Constraint Management136 Questions
Exam 6: Lean Systems166 Questions
Exam 7: Project Management139 Questions
Exam 8: Forecasting150 Questions
Exam 9: Inventory Management205 Questions
Exam 10: Operations Planning and Scheduling149 Questions
Exam 11: Resource Planning124 Questions
Exam 12: Supply Chain Design77 Questions
Exam 13: Supply Chain Logistic Networks114 Questions
Exam 14: Supply Chain Integration120 Questions
Exam 15: Supply Chain Sustainability78 Questions
Exam 16: Supplement A Decision Making107 Questions
Exam 17: Supplement J Operations Scheduling123 Questions
Exam 18: Supplement K Layout39 Questions
Exam 19: Supplement B Waiting Lines111 Questions
Exam 20: Supplement C Special Inventory Models53 Questions
Exam 21: Supplement D Linear Programming87 Questions
Exam 22: Supplement E Simulation54 Questions
Exam 23: Supplement F Financial Analysis55 Questions
Exam 24: Supplement G Acceptance Sampling Plans87 Questions
Exam 25: Supplement H Measuring Output Rates108 Questions
Exam 26: Supplement I Learning Curve Analysis50 Questions
Select questions type
Provide three examples of operations management decision problems for which linear programming can be useful, and why.
(Essay)
4.7/5  (33)
(33)
________ is the amount by which the left-hand side falls short of the right-hand side in a linear programming model.
(Short Answer)
4.9/5  (37)
(37)
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four-ounce portion must contain 22 units of protein, 15 units of vitamin A, and 8 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 6 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 8 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 8 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 5 cents per ounce, and eggs cost 12 cents per ounce. To make the production process as easy as possible, she would like to make exactly four ounces of cat food from her recipe. She used POM for Windows and received the following results. Provide an interpretation.
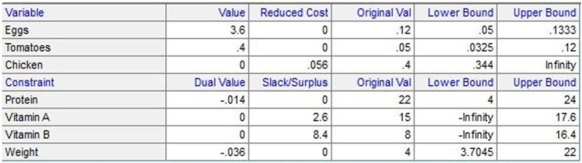
(Essay)
4.8/5  (36)
(36)
Scenario D.1
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four ounce portion must contain 20 units of protein, 15 units of vitamin A, and 10 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 5 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 5 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 5 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 8 cents per ounce, and eggs cost 12 cents per ounce.
-Referring to Scenario D.1, assume that an optimal serving contains 0.89 ounces of chicken and 0.52 ounces of tomatoes. Which of the following statements is best?
(Multiple Choice)
4.8/5  (39)
(39)
One assumption of linear programming is that a decision maker cannot use negative quantities of the parameters.
(True/False)
4.8/5  (26)
(26)
Table D.2
Bahouth Enterprises produces a variety of hookahs for clients around the globe. Their small plant has a highly flexible workforce that can switch between products seamlessly. They forecast using a six-month planning period and have a demand forecast as shown in the table. The per-unit costs for each output option the sales and operations planner has at his disposal are indicated in the table. Regular output costs $40 per unit, overtime production is $60 per unit, and subcontracting is $70 per unit. Holding inventory from one month to the next costs $2 per unit per month and a backlog costs $5 per unit per month. Regular plant capacity is 300 units per month.
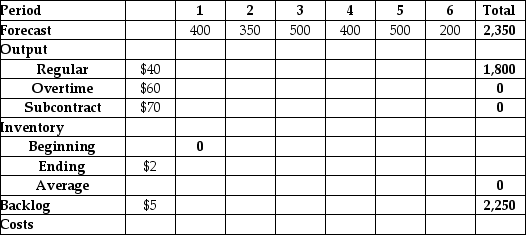 -Use the information in Table D.2. If the planner decides to adopt a level plan for the planning period, what will the regular output be for month 3?
-Use the information in Table D.2. If the planner decides to adopt a level plan for the planning period, what will the regular output be for month 3?
(Multiple Choice)
4.9/5  (33)
(33)
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four ounce portion must contain 22 units of protein, 15 units of vitamin A, and 8 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 6 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 8 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 8 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 5 cents per ounce, and eggs cost 12 cents per ounce. To make the production process as easy as possible, she would like to make exactly four ounces of cat food from her recipe. Formulate this decision as a linear programming problem, defining fully your decision variables and then giving the objective function and constraints.
(Essay)
4.8/5  (37)
(37)
The CZ Jewelry Company produces two products: (1) engagement rings and (2) jeweled watches. The production process for each is similar in that both require a certain number of hours of diamond work and a certain number of labor hours in the gold department. Each ring takes four hours of diamond work and two hours in the gold shop. Each watch requires three hours in diamonds and one hour in the gold department. There are 240 hours of diamond labor available and 100 hours of gold department time available for the next month. Each engagement ring sold yields a profit of $9; each watch produced may be sold for a $10 profit.
a. Give a complete formulation of this problem, including a careful definition of your decision variables. Let the first decision variable, (X₁), deal with rings, the second decision variable, (X₂), with watches, the first constraint with diamonds, and the second constraint with gold.
b. Graph the problem fully in the following space. Label the axes carefully, plot the constraints, shade the feasibility region, plot at least one isoprofit line that reveals the optimal solution, circle the corner points and highlight the optimal corner point so found, and solve for it algebraically. (Show all your work to get credit.)
(Essay)
4.8/5  (29)
(29)
Scenario D.1
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four ounce portion must contain 20 units of protein, 15 units of vitamin A, and 10 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 5 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 5 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 5 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 8 cents per ounce, and eggs cost 12 cents per ounce.
-Referring to Scenario D.1, what is an appropriate constraint for this scenario?
(Multiple Choice)
4.9/5  (33)
(33)
A portfolio manager is trying to balance investments between bonds, stocks and cash. The return on stocks is 12 percent, 9 percent on bonds, and 3 percent on cash. The total portfolio is $1 billion, and he or she must keep 10 percent in cash in accordance with company policy. The fund's prospectus promises that stocks cannot exceed 75 percent of the portfolio, and the ratio of stocks to bonds must equal two. Formulate this investment decision as a linear programming problem, defining fully your decision variables and then giving the objective function and constraints.
(Essay)
4.9/5  (32)
(32)
A small oil company has a refining budget of $200,000 and would like to determine the optimal production plan for profitability. The following table lists the costs associated with its three products.
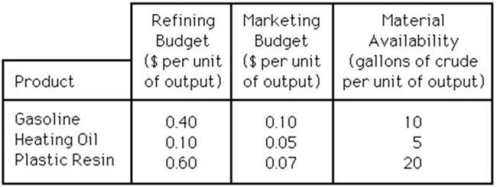 Marketing has a budget of $50,000, and the company has 750,000 gallons of crude oil available. Each gallon of gasoline contributes 14 cents of profits, heating oil provides 10 cents, and plastic resin 30 cents per unit. The refining process results in a ratio of two units of heating oil for each unit of gasoline produced. This problem has been modeled as a linear programming problem and solved on the computer. The set up and output follows:
Marketing has a budget of $50,000, and the company has 750,000 gallons of crude oil available. Each gallon of gasoline contributes 14 cents of profits, heating oil provides 10 cents, and plastic resin 30 cents per unit. The refining process results in a ratio of two units of heating oil for each unit of gasoline produced. This problem has been modeled as a linear programming problem and solved on the computer. The set up and output follows:
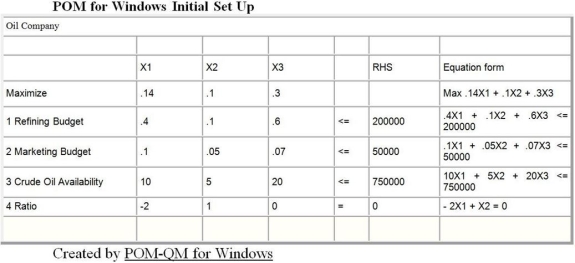
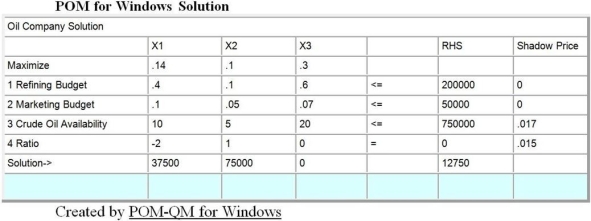
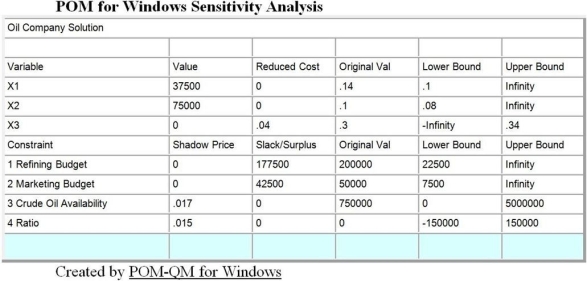 a. Give a linear programming formulation for this problem. Make the variable definitions and constraints line up with the computer output.
b. What product mix maximizes the profit for the company using its limited resources?
c. How much plastic resin is produced if profits are maximized?
d. Give a full explanation of the meaning of the three numbers listed following.
First Number: Slack or surplus of 42,500 for the #2 Marketing Budget constraint.
Second Number: Shadow price of 0 for the #1 Refining Budget constraint.
Third Number: An upper limit of "infinity" for the right-hand-side value for the #1 Refining Budget constraint.
a. Give a linear programming formulation for this problem. Make the variable definitions and constraints line up with the computer output.
b. What product mix maximizes the profit for the company using its limited resources?
c. How much plastic resin is produced if profits are maximized?
d. Give a full explanation of the meaning of the three numbers listed following.
First Number: Slack or surplus of 42,500 for the #2 Marketing Budget constraint.
Second Number: Shadow price of 0 for the #1 Refining Budget constraint.
Third Number: An upper limit of "infinity" for the right-hand-side value for the #1 Refining Budget constraint.
(Essay)
4.8/5  (23)
(23)
Degeneracy occurs when the linear program model consists of only an infeasible region.
(True/False)
4.9/5  (30)
(30)
The ________ is the upper and lower limit of an objective function coefficient over which the optimal values of the decision variables remain unchanged.
(Short Answer)
4.8/5  (27)
(27)
Table D.2
Bahouth Enterprises produces a variety of hookahs for clients around the globe. Their small plant has a highly flexible workforce that can switch between products seamlessly. They forecast using a six-month planning period and have a demand forecast as shown in the table. The per-unit costs for each output option the sales and operations planner has at his disposal are indicated in the table. Regular output costs $40 per unit, overtime production is $60 per unit, and subcontracting is $70 per unit. Holding inventory from one month to the next costs $2 per unit per month and a backlog costs $5 per unit per month. Regular plant capacity is 300 units per month.
 -Use the information in Table D.2. The plant has no limits on the number of units produced by overtime or subcontractors and adopts a level plan strategy for the six-month planning period. What is the cost for month 6 of their level plan?
-Use the information in Table D.2. The plant has no limits on the number of units produced by overtime or subcontractors and adopts a level plan strategy for the six-month planning period. What is the cost for month 6 of their level plan?
(Multiple Choice)
4.9/5  (38)
(38)
A(n) ________ is a value that the decision maker cannot control and that does not change when the solution is implemented.
(Short Answer)
4.9/5  (32)
(32)
While glancing over the sensitivity report, you note that the stitching labor has a shadow price of $10 and a lower limit of 24 hours with an upper limit of 36 hours. If your original right hand value for stitching labor was 30 hours, you know that:
(Multiple Choice)
4.9/5  (32)
(32)
Table D.3
The Harper Company is in the process of production planning for the next four quarters. The company follows a policy of a stable workforce and uses overtime and subcontracting to meet uneven forecasted demand. Anticipation inventory is also allowed, but not backorders. Undertime is paid, at a rate of $5.00 per unit. The beginning (or current) inventory is 25 units. Details are shown in the following POM for Windows table.
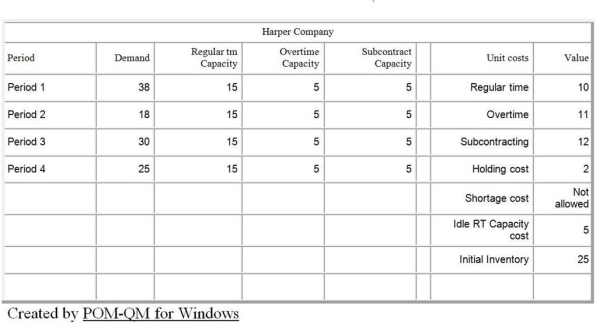
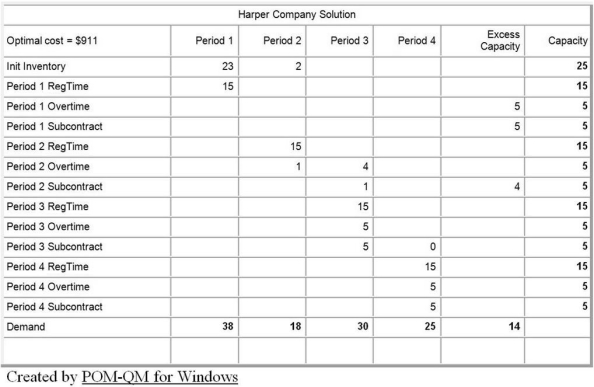 -Use the information in Table D.3. Given the information in the optimal tableau, what is the demand forecast for quarter 2?
-Use the information in Table D.3. Given the information in the optimal tableau, what is the demand forecast for quarter 2?
(Multiple Choice)
4.8/5  (43)
(43)
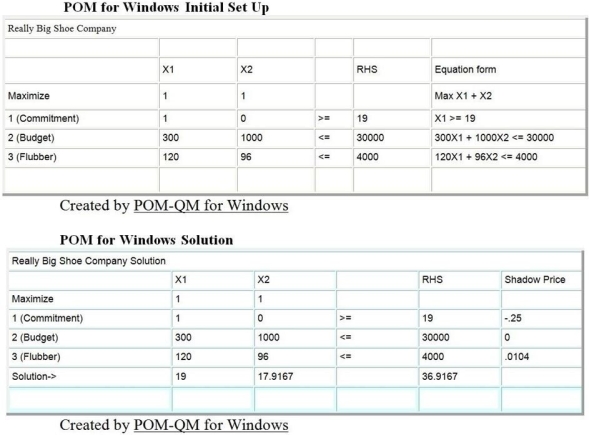
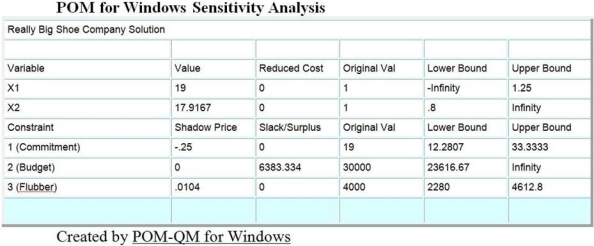
The Really Big Shoe Company is a manufacturer of basketball shoes and football shoes. Ed Sullivan, the manager of marketing, must decide the best way to spend advertising resources. Each football team sponsored requires 120 pairs of shoes. Each basketball team requires 32 pairs of shoes. Football coaches receive $300,000 for shoe sponsorship and basketball coaches receive $1,000,000. Ed's promotional budget is $30,000,000. The Really Big Shoe Company has a very limited supply (4 liters or 4,000cc) of flubber, a rare and costly raw material used only in promotional athletic shoes. Each pair of basketball shoes requires 3cc of flubber, and each pair of football shoes requires 1cc of flubber. Ed desires to sponsor as many basketball and football teams as resources allow. However, he has already committed to sponsoring 19 football teams and wants to keep his promises.
a. Give a linear programming formulation for Ed. Make the variable definitions and constraints line up with the computer output appended to this exam.
b. Solve the problem graphically, showing constraints, feasible region, and isoprofit lines. Circle the optimal solution, making sure that the isoprofit lines drawn make clear why you chose this point. (Show all your calculations for plotting the constraints and isoprofit line on the left to get credit.)
 c. Solve algebraically for the corner point on the feasible region.
d. Part of Ed's computer output is shown following. Give a full explanation of the meaning of the three numbers listed below. Based on your graphical and algebraic analysis, explain why these numbers make sense. (Hint: He formulated the budget constraint in terms of $000.) See the computer printout that follows.
First Number: The shadow price of 0.0104 for the "Flubber" constraint.
Second Number: The slack or surplus of 6383.334 for the "Budget" constraint.
Third Number: The lower limit of 12.2807 for the "Commitment" constraint.
c. Solve algebraically for the corner point on the feasible region.
d. Part of Ed's computer output is shown following. Give a full explanation of the meaning of the three numbers listed below. Based on your graphical and algebraic analysis, explain why these numbers make sense. (Hint: He formulated the budget constraint in terms of $000.) See the computer printout that follows.
First Number: The shadow price of 0.0104 for the "Flubber" constraint.
Second Number: The slack or surplus of 6383.334 for the "Budget" constraint.
Third Number: The lower limit of 12.2807 for the "Commitment" constraint.
(Essay)
4.8/5  (39)
(39)
In linear programming, each parameter is assumed to be known with certainty.
(True/False)
4.8/5  (30)
(30)
Scenario D.1
Lisa lives out in the country with her seven cats and avoids driving into the big city as much as possible. She has decided to make her own cat food and has the following nutritional guidelines. Each four ounce portion must contain 20 units of protein, 15 units of vitamin A, and 10 units of vitamin B. She has eggs, tomatoes, and chicken meat as possible inputs to her cat food. Each ounce of eggs contains 5 units of protein, 4 units of Vitamin A, and 3 units of Vitamin B. Each ounce of tomatoes contains 1 unit of protein, 5 units of Vitamin A, and 14 units of Vitamin B. Each ounce of chicken contains 22 units of protein, 14 units of Vitamin A, and 5 units of Vitamin B. Chicken costs 40 cents per ounce, tomatoes cost 8 cents per ounce, and eggs cost 12 cents per ounce.
-Referring to Scenario D.1, what is an appropriate objective function for this scenario?
(Multiple Choice)
4.9/5  (29)
(29)
Showing 41 - 60 of 87
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)