Exam 11: Vectors in the Plane
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
To carry a 100-pound cylindrical weight, two workers lift on the ends of short ropes tied to an eyelet on the top center of the cylinder. One rope makes a angle away from the vertical and the other makes a angle as shown in the figure below. Find each rope's tension if the resultant force is vertical.Round your answer to two decimal places.
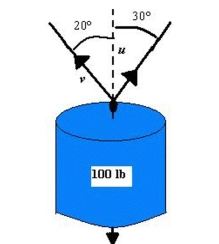
(Multiple Choice)
4.9/5  (41)
(41)
Find the length of the minor axis of the ellipse generated when the surface is intersected by the plane
(Multiple Choice)
4.9/5  (32)
(32)
Find an equation in rectangular coordinates for the equation given in spherical coordinates.
(Multiple Choice)
4.8/5  (41)
(41)
Find the direction angles of the vector u given below. Round your answer to one decimal place.
(Multiple Choice)
4.8/5  (42)
(42)
Assume the only force to overcome is that due to gravity. Find the force perpendicular to the hill. Round your answer to one decimal place. 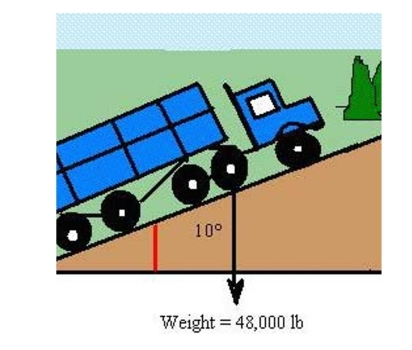
(Multiple Choice)
5.0/5  (36)
(36)
A child applies the brakes on a bicycle by applying a downward force of 25 pounds on the pedal when the crank makes a angle with the horizontal (see figure). The crank is 6 inches in length. Find the torque at . Round your answer to two decimal places.
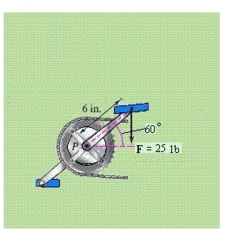
(Multiple Choice)
4.7/5  (37)
(37)
Determine whether the following planes are parallel, orthogonal, or neither. If they are neither parallel nor orthogonal, find the angle of intersection. -2x-31y+5z+3=0 -3x+y+5z-4=0
(Multiple Choice)
4.9/5  (43)
(43)
To carry a 500-pound cylindrical weight, two workers lift on the ends of short ropes tied to an eyelet on the top center of the cylinder. One rope makes a angle away from the vertical and the other makes a angle as shown in the figure below. Find the vertical component of each worker's force. Round your answer to two decimal places.
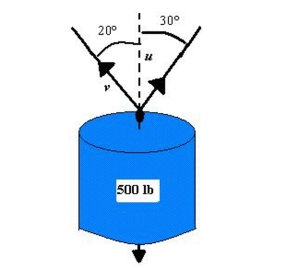
(Multiple Choice)
4.8/5  (32)
(32)
Find the vector v whose initial and terminal points are given below.
(Multiple Choice)
4.8/5  (44)
(44)
Find an equation of a plane passing through the given point and perpendicular to the given vector. Point: Vector:
(Multiple Choice)
4.7/5  (47)
(47)
Identify the equation (written in terms of cylindrical or spherical coordinates) of the following graph. 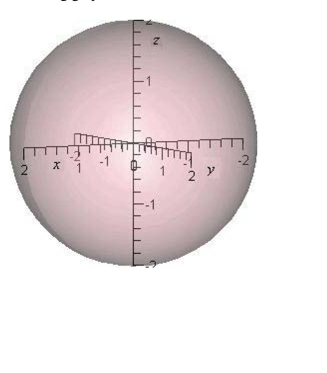
(Multiple Choice)
4.7/5  (29)
(29)
Find a set of parametric equations of the line through the point the vector .
(Multiple Choice)
4.9/5  (33)
(33)
The top of a rubber bushing designed to absorb vibrations in an automobile is the surface of revolution generated by revolving the curve about the z-axis. The bushing has a hole of 4 centimeters in diameter through its center and parallel to the axis of revolution. All measurements are in centimeters and the bushing is set on the xy-plane. Find the volume of the rubber bushing. Round your answer to two decimal places.
(Multiple Choice)
4.6/5  (32)
(32)
Find an equation of the surface of revolution generated by revolving the curve given below in the indicated coordinate plane about the given axis. Equation of Curve Coordinate Plane Axis of Revolution z=5x xz -plane z -axis
(Multiple Choice)
4.9/5  (33)
(33)
Find vectors u and v whose initial and terminal points are given. Determine whether u and v are equivalent.
(Multiple Choice)
4.8/5  (45)
(45)
Showing 21 - 40 of 125
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)