Question 1

$\text { Find the derivative of the function } f ( x ) = - 7 x ^ { 3 } + 4 x ^ { 2 } + 1 \text {. }$

Accepted Answer

A)  $f ^ { t } ( x ) = - 14 x + 4 x ^ { 2 }$ 
B)  $f ^ { t} ( x ) = - 14 x ^ { 2 } + 4 x$ 
C)  $f ^ { t } ( x ) = - 7 x ^ { 2 } + 4 x ^ { 2 } + 1$ 
D)  $f ^ { t } ( x ) = - 21 x ^ { 2 } + 8 x + 1$ 
E)  $f ^ {t } ( x ) = - 21 x ^ { 2 } + 8 x$ 
A)  $f ^ { t } ( x ) = - 14 x + 4 x ^ { 2 }$ 
B)  $f ^ { t} ( x ) = - 14 x ^ { 2 } + 4 x$ 
C)  $f ^ { t } ( x ) = - 7 x ^ { 2 } + 4 x ^ { 2 } + 1$ 
D)  $f ^ { t } ( x ) = - 21 x ^ { 2 } + 8 x + 1$ 
E)  $f ^ {t } ( x ) = - 21 x ^ { 2 } + 8 x$ E

Question 2

$\text { Find the slope-intercept equation of the line tangent to the graph of } y = e ^ { x } \text { when }$ $x = \ln 3$

Accepted Answer

A)  $y = \ln ( 3 ) x + 3$ 
B)  $y = \ln ( 3 ) x + 3 ( 1 - \ln 3 )$ 
C)  $y = \ln ( 3 ) x - 3$ 
D)  $y = 3 x + 3 ( 1 - \ln 3 )$ 
E)  $y = 3 x - 3 ( 1 - \ln 3 )$ 
A)  $y = \ln ( 3 ) x + 3$ 
B)  $y = \ln ( 3 ) x + 3 ( 1 - \ln 3 )$ 
C)  $y = \ln ( 3 ) x - 3$ 
D)  $y = 3 x + 3 ( 1 - \ln 3 )$ 
E)  $y = 3 x - 3 ( 1 - \ln 3 )$ D

Question 3

$\text { Suppose that an automobile's velocity starting from rest is } v ( t ) = \frac { 240 t } { 5 t + 13 } \text { where } v \text { is }$ measured in feet per second. Find the acceleration at 9 seconds. Round your answer to one decimal place.

Accepted Answer

A)  $1.9 \mathrm { ft } / \mathrm { sec } ^ { 2 }$ 
B)  $0.9 \mathrm { ft } / \mathrm { sec } ^ { 2 }$ 
C)  $0.6 \mathrm { ft } / \mathrm { sec } ^ { 2 }$ 
D)  $0.2 \mathrm { ft } / \mathrm { sec } ^ { 2 }$ 
E)  $8.3 \mathrm { ft } / \mathrm { sec } ^ { 2 }$ 
A)  $1.9 \mathrm { ft } / \mathrm { sec } ^ { 2 }$ 
B)  $0.9 \mathrm { ft } / \mathrm { sec } ^ { 2 }$ 
C)  $0.6 \mathrm { ft } / \mathrm { sec } ^ { 2 }$ 
D)  $0.2 \mathrm { ft } / \mathrm { sec } ^ { 2 }$ 
E)  $8.3 \mathrm { ft } / \mathrm { sec } ^ { 2 }$ B

Question 4

Assume that x and y are both differentiable functions of t . Find $\frac { d y } { d t }$ when $x = 49$ and $\frac { d x } { d t } = 17$ for the equation $y = \sqrt { x }$.

Accepted Answer

A)  $\frac { d y } { d t } = \frac { 17 } { 14 }$ 
B)  $\frac { d y } { d t } = 14$ 
C)  $\frac { d y } { d t } = \frac { 14 } { 17 }$ 
D)  $\frac { d y } { d t } = - \frac { 17 } { 14 }$ 
E)  $\frac { d y } { d t } = - 14$ 
A)  $\frac { d y } { d t } = \frac { 17 } { 14 }$ 
B)  $\frac { d y } { d t } = 14$ 
C)  $\frac { d y } { d t } = \frac { 14 } { 17 }$ 
D)  $\frac { d y } { d t } = - \frac { 17 } { 14 }$ 
E)  $\frac { d y } { d t } = - 14$

Question 5

$\text { Find } \frac { d ^ { 2 } y } { d x ^ { 2 } } \text { in terms of } x \text { and } y \text { given that } 3 - 7 x y = 3 x - 7 y$

Accepted Answer

A) $\frac { d ^ { 2 } y } { d x ^ { 2 } } = 0$ 
B)  $\frac { d ^ { 2 } y } { d x ^ { 2 } } = - 7 y ^ { 3 }$ 
C)  $\frac { d ^ { 2 } y } { d x ^ { 2 } } = - 7 y ^ { 2 }$ 
D)  $\frac { d ^ { 2 } y } { d x ^ { 2 } } = 3 y ^ { 2 }$ 
E)  $\frac { d ^ { 2 } y } { d x ^ { 2 } } = - 3 y ^ { 3 }$ 
A) $\frac { d ^ { 2 } y } { d x ^ { 2 } } = 0$ 
B)  $\frac { d ^ { 2 } y } { d x ^ { 2 } } = - 7 y ^ { 3 }$ 
C)  $\frac { d ^ { 2 } y } { d x ^ { 2 } } = - 7 y ^ { 2 }$ 
D)  $\frac { d ^ { 2 } y } { d x ^ { 2 } } = 3 y ^ { 2 }$ 
E)  $\frac { d ^ { 2 } y } { d x ^ { 2 } } = - 3 y ^ { 3 }$

Question 6

Find the derivative of the function. $$f ( x ) = \frac { 1 } { x ^ { 8 } }$$

Accepted Answer

A)  $f ^ { t } ( x ) = - \frac { 9 } { x ^ { 9 } }$ 
B) $f ^ { t } ( x ) = - \frac { 8 } { x ^ { 7 } }$ 
C)  $f ^ { t} ( x ) = \frac { 8 } { x ^ { 9 } }$ 
D)  $f ^ { t } ( x ) = - \frac { 8 } { x ^ { 9 } }$ 
E) $f ^ { t } ( x ) = - \frac { 7 } { x ^ { 9 } }$ 
A)  $f ^ { t } ( x ) = - \frac { 9 } { x ^ { 9 } }$ 
B) $f ^ { t } ( x ) = - \frac { 8 } { x ^ { 7 } }$ 
C)  $f ^ { t} ( x ) = \frac { 8 } { x ^ { 9 } }$ 
D)  $f ^ { t } ( x ) = - \frac { 8 } { x ^ { 9 } }$ 
E) $f ^ { t } ( x ) = - \frac { 7 } { x ^ { 9 } }$

Question 7

$\text { Evaluate the derivative of the function } y = \sqrt [ 5 ] { 2 x ^ { 5 } + 2 x } \text { at the point } x = 3 \text {. }$

Accepted Answer

A) $y ^ { t } ( 3 ) = \frac { 812 } { ( 492 ) ^ { \frac { 3 } { 5 } } }$ 
B)  $y ^ { t } ( 3 ) = \frac { 812 } { 5 ( 492 ) ^ { \frac { 3 } { 5 } } }$ 
C)  $y ^ { t } ( 3 ) = \frac { 812 } { 5 ( 492 ) ^ { \frac { 4 } { 5 } } }$ 
D) $y ^ { t } ( 3 ) = \frac { 812 } { 407 ( 492 ) ^ { \frac { 4 } { 5 } } }$ 
E) $y ^ { t } ( 3 ) = \frac { 812 } { 5 ( 492 ) ^ { \frac { 6 } { 5 } } }$ 
A) $y ^ { t } ( 3 ) = \frac { 812 } { ( 492 ) ^ { \frac { 3 } { 5 } } }$ 
B)  $y ^ { t } ( 3 ) = \frac { 812 } { 5 ( 492 ) ^ { \frac { 3 } { 5 } } }$ 
C)  $y ^ { t } ( 3 ) = \frac { 812 } { 5 ( 492 ) ^ { \frac { 4 } { 5 } } }$ 
D) $y ^ { t } ( 3 ) = \frac { 812 } { 407 ( 492 ) ^ { \frac { 4 } { 5 } } }$ 
E) $y ^ { t } ( 3 ) = \frac { 812 } { 5 ( 492 ) ^ { \frac { 6 } { 5 } } }$

Question 8

$\text { Evaluate } \frac { d y } { d x } \text { for the equation } \tan ( 10 x + 8 y ) = 10 x \text { at the given point } ( 0,0 )$ Round your answer to two decimal places.

Accepted Answer

A)  $\frac { d y } { d x } = 1.38$ 
B)  $\frac { d y } { d x } = - 1.00$ 
C)  $\frac { d y } { d x } = - 9.00$ 
D)  $\frac { d y } { d x } = - 1.13$ 
E)  $\frac { d y } { d x } = 1.50$ 
A)  $\frac { d y } { d x } = 1.38$ 
B)  $\frac { d y } { d x } = - 1.00$ 
C)  $\frac { d y } { d x } = - 9.00$ 
D)  $\frac { d y } { d x } = - 1.13$ 
E)  $\frac { d y } { d x } = 1.50$

Question 9

$\text { Find the derivative of the function } f ( x ) = \operatorname { arcsec } ( 9 x ) \text {. }$

Accepted Answer

A) $-\frac { 1 } { | 9 x | \sqrt { 81 x ^ { 2 } - 1 } }$ 
B) $ \frac { 1 } { | x | \sqrt { 81 x ^ { 2 } - 1 } }$ 
C) $\frac { 1 } { | 9 x | \sqrt { 81 x ^ { 2 } - 1 } }$ 
D) $\frac { 1 } { \sqrt { 81 x ^ { 2 } + 1 } }$ 
E) $- \frac { 1 } { | x | \sqrt { 81 x ^ { 2 } - 1 } }$ 
A) $-\frac { 1 } { | 9 x | \sqrt { 81 x ^ { 2 } - 1 } }$ 
B) $ \frac { 1 } { | x | \sqrt { 81 x ^ { 2 } - 1 } }$ 
C) $\frac { 1 } { | 9 x | \sqrt { 81 x ^ { 2 } - 1 } }$ 
D) $\frac { 1 } { \sqrt { 81 x ^ { 2 } + 1 } }$ 
E) $- \frac { 1 } { | x | \sqrt { 81 x ^ { 2 } - 1 } }$

Question 10

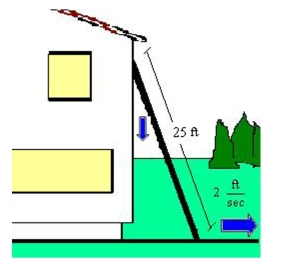
A ladder feet long is leaning against the wall of a house (see figure). The base of the ladder is pulled away from the wall at a rate of feet per second. Consider the triangle formed by The side of the house, the ladder, and the ground. Find the rate at which the area of the triangle is Changed when the base of the ladder is feet from the wall. Round your answer to two decimal Places.

Accepted Answer

A)  $16.67 \mathrm { ft } ^ { 2 } / \mathrm { sec }$ 
B)  $119.10 \mathrm { ft } ^ { 2 } / \mathrm { sec }$ 
C)  $66.34 \mathrm { ft } ^ { 2 } / \mathrm { sec }$ 
D)  $20.06 \mathrm { ft } ^ { 2 } / \mathrm { sec }$ 
E)  $40.13 \mathrm { ft } ^ { 2 } / \mathrm { sec }$ 
A)  $16.67 \mathrm { ft } ^ { 2 } / \mathrm { sec }$ 
B)  $119.10 \mathrm { ft } ^ { 2 } / \mathrm { sec }$ 
C)  $66.34 \mathrm { ft } ^ { 2 } / \mathrm { sec }$ 
D)  $20.06 \mathrm { ft } ^ { 2 } / \mathrm { sec }$ 
E)  $40.13 \mathrm { ft } ^ { 2 } / \mathrm { sec }$

Question 11

$\text { Find } \frac { d y } { d t } \text { when } x = \frac { \pi } { 7 } \text {. }$

Accepted Answer

A)  $\frac { d y } { d t } = 6 \cos \frac { 2 \pi } { 7 }$ 
B)  $\frac { d y } { d t } = 12 \cos \frac { 6 \pi } { 7 }$ 
C)  $\frac { d y } { d t } = 6 \cos \frac { 6 \pi } { 7 }$ 
D)  $\frac { d y } { d t } = 12 \cos \frac { 2 \pi } { 7 }$ 
E)  $\frac { d y } { d t } = 12 \cos \frac { 12 \pi } { 7 }$ 
A)  $\frac { d y } { d t } = 6 \cos \frac { 2 \pi } { 7 }$ 
B)  $\frac { d y } { d t } = 12 \cos \frac { 6 \pi } { 7 }$ 
C)  $\frac { d y } { d t } = 6 \cos \frac { 6 \pi } { 7 }$ 
D)  $\frac { d y } { d t } = 12 \cos \frac { 2 \pi } { 7 }$ 
E)  $\frac { d y } { d t } = 12 \cos \frac { 12 \pi } { 7 }$

Question 12

Find an equation of the tangent line to the graph of the function $( y - 6 ) ^ { 2 } = 5 ( x - 5 )$ at the point $( 8.20,2.00 )$. The coefficients below are given to two decimal places.

Accepted Answer

A)  $y = - 0.63 x + 7.13$ 
B)  $y = 3.38 x + 25.68$ 
C)  $y = 3.38 x - 25.68$ 
D)  $y = - 0.63 x + 25.68$ 
E)  $y = 0.63 x + 7.13$ 
A)  $y = - 0.63 x + 7.13$ 
B)  $y = 3.38 x + 25.68$ 
C)  $y = 3.38 x - 25.68$ 
D)  $y = - 0.63 x + 25.68$ 
E)  $y = 0.63 x + 7.13$

Question 13

$\text { Find an equation of the line that is tangent to the graph of } f \text { and parallel to the given }$ line.
$f ( x ) = 3 x ^ { 3 } , 9 x - y + 9 = 0$

Accepted Answer

A)  $y = - 9 x + 6$ 
B)  $y = - 3 x + 6$ 
C)  $y = 9 x - 3$ and $y = 9 x + 3$ 
D)  $y = - 9 x - 6$ 
E)  $y = 9 x - 6$ and $y = 9 x + 6$ 
A)  $y = - 9 x + 6$ 
B)  $y = - 3 x + 6$ 
C)  $y = 9 x - 3$ and $y = 9 x + 3$ 
D)  $y = - 9 x - 6$ 
E)  $y = 9 x - 6$ and $y = 9 x + 6$

Question 14

$\text { Find } \frac { d y } { d x } \text { by implicit differentiation given that } x ^ { \frac { 8 } { 9 } } + y ^ { \frac { 8 } { 9 } } = 2 \text {. }$

Accepted Answer

A)  $\frac { d y } { d x } = - \sqrt [ 9 ] { x y }$ 
B)  $\frac { d y } { d x } = \sqrt [ 9 ] { \frac { y } { x } }$ 
C)  $\frac { d y } { d x } = - 9 \sqrt { \frac { y } { x } }$ 
D)  $\frac { d y } { d x } = \sqrt [ 9 ] { x y }$ 
E)  $\frac { d y } { d x } = - 9 \sqrt { \frac { x } { y } }$ 
A)  $\frac { d y } { d x } = - \sqrt [ 9 ] { x y }$ 
B)  $\frac { d y } { d x } = \sqrt [ 9 ] { \frac { y } { x } }$ 
C)  $\frac { d y } { d x } = - 9 \sqrt { \frac { y } { x } }$ 
D)  $\frac { d y } { d x } = \sqrt [ 9 ] { x y }$ 
E)  $\frac { d y } { d x } = - 9 \sqrt { \frac { x } { y } }$

Question 15

$\text { Suppose the table below shows the temperature } T \left( { } ^ { \circ } \bar { F } \right) \text { at which a given liquid boils }$ at selected pressures $p$ (pounds per square inch). A model that approximates the data is $T = 107.97 + 64.96 \ln p + 9.91 \sqrt { p }$. Find the rate of change of $T$ with respect to $p$ when $P = 20$. Round your answer to two decimal places.
$\begin{array}{|r|r|r|r|r|r|r|r|r|r|}
\hline P & 5 & 10 & \begin{array}{c}
14.696 \
(1 \mathrm{~atm})
\end{array} & 20 & 30 & 40 & 60 & 80 & 100 \
\hline T & 234.68 & 288.88 & 320.55 & 346.89 & 383.19 & 410.28 & 450.7 & 481.26 & 506.22 \
\hline
\end{array}$

Accepted Answer

A)  $113.43 \mathrm { deg } / \mathrm { lb } / \mathrm { in } ^ { 2 }$ 
B)  $4.36 \mathrm { deg } / \mathrm { lb } / \mathrm { in } ^ { 2 }$ 
C)  $5.46 \mathrm { deg } / \mathrm { lb } / \mathrm { in } ^ { 2 }$ 
D)  $112.33 \mathrm { deg } / \mathrm { lb } / \mathrm { in } ^ { 2 }$ 
E)  $1.11 \mathrm { deg } / \mathrm { lb } / \mathrm { in } ^ { 2 }$ 
A)  $113.43 \mathrm { deg } / \mathrm { lb } / \mathrm { in } ^ { 2 }$ 
B)  $4.36 \mathrm { deg } / \mathrm { lb } / \mathrm { in } ^ { 2 }$ 
C)  $5.46 \mathrm { deg } / \mathrm { lb } / \mathrm { in } ^ { 2 }$ 
D)  $112.33 \mathrm { deg } / \mathrm { lb } / \mathrm { in } ^ { 2 }$ 
E)  $1.11 \mathrm { deg } / \mathrm { lb } / \mathrm { in } ^ { 2 }$

Question 16

Use the Product Rule to differentiate. $f ( t ) = t ^ { - 3 } \cos t$

Accepted Answer

A)  $f ( t ) = - t ^ { - 3 } \sin t + 3 t ^ { - 4 } \cos t$ 
B)  $f ^ { t } ( t ) = 3 t ^ { - 2 } \cos t - t ^ { - 3 } \sin t$ 
C)  $f ^ { t } ( t ) = t ^ { - 3 } \sin t - 3 t ^ { - 4 } \cos t$ 
D)  $f ^ {t } ( t ) = - t ^ { - 3 } \sin t - 3 t ^ { - 4 } \cos t$ 
E)  $f ^ { t } ( t ) = - t ^ { - 3 } \sin t + 3 t ^ { - 4 } \sin t$ 
A)  $f ( t ) = - t ^ { - 3 } \sin t + 3 t ^ { - 4 } \cos t$ 
B)  $f ^ { t } ( t ) = 3 t ^ { - 2 } \cos t - t ^ { - 3 } \sin t$ 
C)  $f ^ { t } ( t ) = t ^ { - 3 } \sin t - 3 t ^ { - 4 } \cos t$ 
D)  $f ^ {t } ( t ) = - t ^ { - 3 } \sin t - 3 t ^ { - 4 } \cos t$ 
E)  $f ^ { t } ( t ) = - t ^ { - 3 } \sin t + 3 t ^ { - 4 } \sin t$

Question 17

$\text { Find the derivative of the function } f ( x ) = \frac { e ^ { x } - 4 } { e ^ { x } + 4 } \text {. Simplify your answer. }$

Accepted Answer

A) $\frac { 2 e ^ { 2 x } } { \left( e ^ { x } + 4 \right) ^ { 2 } }$ 
B) $\frac { - 8 e ^ { x } } { \left( e ^ { x } + 4 \right) ^ { 2 } }$ 
C) $\frac { 8 e ^ { x } } { \left( e ^ { x } + 4 \right) ^ { 2 } }$ 
D)  $\frac { 2 e ^ { 2 x } + 8 e ^ { x } } { \left( e ^ { x } + 4 \right) ^ { 2 } }$ 
E) $\frac { 1 } { \left( e ^ { x } + 4 \right) ^ { 2 } }$ 
A) $\frac { 2 e ^ { 2 x } } { \left( e ^ { x } + 4 \right) ^ { 2 } }$ 
B) $\frac { - 8 e ^ { x } } { \left( e ^ { x } + 4 \right) ^ { 2 } }$ 
C) $\frac { 8 e ^ { x } } { \left( e ^ { x } + 4 \right) ^ { 2 } }$ 
D)  $\frac { 2 e ^ { 2 x } + 8 e ^ { x } } { \left( e ^ { x } + 4 \right) ^ { 2 } }$ 
E) $\frac { 1 } { \left( e ^ { x } + 4 \right) ^ { 2 } }$

Question 18

$\text { Find } \frac { d y } { d x } \text { by implicit differentiation. }$ $\sin x + 7 \cos 14 y = 2$

Accepted Answer

A)  $\frac { d y } { d x } = \frac { \cos x } { 98 \cos 14 y }$ 
B)  $\frac { d y } { d x } = \frac { \cos x } { 98 \sin 14 y }$ 
C)  $\frac { d y } { d x } = \frac { \cos x } { 14 \sin 14 y }$ 
D)  $\frac { d y } { d x } = \frac { \cos x } { 98 \sin y }$ 
E)  $\frac { d y } { d x } = - \frac { \cos x } { 98 \sin 14 y }$ 
A)  $\frac { d y } { d x } = \frac { \cos x } { 98 \cos 14 y }$ 
B)  $\frac { d y } { d x } = \frac { \cos x } { 98 \sin 14 y }$ 
C)  $\frac { d y } { d x } = \frac { \cos x } { 14 \sin 14 y }$ 
D)  $\frac { d y } { d x } = \frac { \cos x } { 98 \sin y }$ 
E)  $\frac { d y } { d x } = - \frac { \cos x } { 98 \sin 14 y }$

Question 19

$\text { Find the derivative of the function } h ( t ) = 2 \sin ( \arccos t ) \text {. }$

Accepted Answer

A)  $\frac { 2 } { \sqrt { 1 - t ^ { 2 } } }$ 
B)  $2 t \sqrt { 1 - t ^ { 2 } }$ 
C)  $- \frac { 2 t } { \sqrt { 1 - t ^ { 2 } } }$ 
D)  $\frac { t } { \sqrt { 1 + t ^ { 2 } } }$ 
E)  $2 t \sqrt { 1 + t ^ { 2 } }$ 
A)  $\frac { 2 } { \sqrt { 1 - t ^ { 2 } } }$ 
B)  $2 t \sqrt { 1 - t ^ { 2 } }$ 
C)  $- \frac { 2 t } { \sqrt { 1 - t ^ { 2 } } }$ 
D)  $\frac { t } { \sqrt { 1 + t ^ { 2 } } }$ 
E)  $2 t \sqrt { 1 + t ^ { 2 } }$

Question 20

Newton's Method to approximate the x-value of the indicated point of intersection of the two graphs accurate to three decimal places.Continue the process until two $\text { successive approximations differ by less than } 0.001 \text {. [Hint: Let } h ( x ) = f ( x ) - g ( x ) \text {.] }$
$\begin{array}{l}
f(x)=3-x \
g(x)=\frac{1}{\sqrt{x^{2}+4}}
\end{array}$

Accepted Answer

A) 2.651 
B) 2.703 
C) 2.660 
D) 2.764 
E) 2.600 
A) 2.651 
B) 2.703 
C) 2.660 
D) 2.764 
E) 2.600

$\text { Find the derivative of the function } f ( x ) = - 7 x ^ { 3 } + 4 x ^ { 2 } + 1 \text {. }$

$\text { Find the slope-intercept equation of the line tangent to the graph of } y = e ^ { x } \text { when }$ $x = \ln 3$

$\text { Suppose that an automobile's velocity starting from rest is } v ( t ) = \frac { 240 t } { 5 t + 13 } \text { where } v \text { is }$ measured in feet per second. Find the acceleration at 9 seconds. Round your answer to one decimal place.

Assume that x and y are both differentiable functions of t . Find $\frac { d y } { d t }$ when $x = 49$ and $\frac { d x } { d t } = 17$ for the equation $y = \sqrt { x }$ .

$\text { Find } \frac { d ^ { 2 } y } { d x ^ { 2 } } \text { in terms of } x \text { and } y \text { given that } 3 - 7 x y = 3 x - 7 y$

Find the derivative of the function. $f ( x ) = \frac { 1 } { x ^ { 8 } }$

$\text { Evaluate the derivative of the function } y = \sqrt [ 5 ] { 2 x ^ { 5 } + 2 x } \text { at the point } x = 3 \text {. }$

$\text { Evaluate } \frac { d y } { d x } \text { for the equation } \tan ( 10 x + 8 y ) = 10 x \text { at the given point } ( 0,0 )$ Round your answer to two decimal places.

$\text { Find the derivative of the function } f ( x ) = \operatorname { arcsec } ( 9 x ) \text {. }$

$\text { Find } \frac { d y } { d t } \text { when } x = \frac { \pi } { 7 } \text {. }$

Find an equation of the tangent line to the graph of the function $( y - 6 ) ^ { 2 } = 5 ( x - 5 )$ at the point $( 8.20,2.00 )$ . The coefficients below are given to two decimal places.

$\text { Find an equation of the line that is tangent to the graph of } f \text { and parallel to the given }$ line. $f ( x ) = 3 x ^ { 3 } , 9 x - y + 9 = 0$

$\text { Find } \frac { d y } { d x } \text { by implicit differentiation given that } x ^ { \frac { 8 } { 9 } } + y ^ { \frac { 8 } { 9 } } = 2 \text {. }$

Use the Product Rule to differentiate. $f ( t ) = t ^ { - 3 } \cos t$

$\text { Find the derivative of the function } f ( x ) = \frac { e ^ { x } - 4 } { e ^ { x } + 4 } \text {. Simplify your answer. }$

$\text { Find } \frac { d y } { d x } \text { by implicit differentiation. }$ $\sin x + 7 \cos 14 y = 2$

$\text { Find the derivative of the function } h ( t ) = 2 \sin ( \arccos t ) \text {. }$

Graphs and Models

A Preview of Calculus

Extrema on an Interval

Antiderivatives and Indefinite Integration

Slope Fields and Eulers Method

Area of a Region Between Two Curves

Basic Integration Rules

Sequences

Conics and Calculus

Vectors in the Plane

Vector-Valued Functions

Introduction to Functions of Several Variables

Iterated Integrals and Area in the Plane

Vector Fields

Exact First-Order Equations

Filters

Exam 3: The Derivative and the Tangent Line Problem

Find the derivative of the function f(x)=−7x3+4x2+1. \text { Find the derivative of the function } f ( x ) = - 7 x ^ { 3 } + 4 x ^ { 2 } + 1 \text {. } Find the derivative of the function f(x)=−7x3+4x2+1.

Find the slope-intercept equation of the line tangent to the graph of y=ex when \text { Find the slope-intercept equation of the line tangent to the graph of } y = e ^ { x } \text { when } Find the slope-intercept equation of the line tangent to the graph of y=ex when x=ln⁡3x = \ln 3x=ln3

Assume that x and y are both differentiable functions of t . Find dydt\frac { d y } { d t }dtdy​ when x=49x = 49x=49 and dxdt=17\frac { d x } { d t } = 17dtdx​=17 for the equation y=xy = \sqrt { x }y=x​ .

Find d2ydx2 in terms of x and y given that 3−7xy=3x−7y\text { Find } \frac { d ^ { 2 } y } { d x ^ { 2 } } \text { in terms of } x \text { and } y \text { given that } 3 - 7 x y = 3 x - 7 y Find dx2d2y​ in terms of x and y given that 3−7xy=3x−7y

Find the derivative of the function. f(x)=1x8f ( x ) = \frac { 1 } { x ^ { 8 } }f(x)=x81​

Evaluate the derivative of the function y=2x5+2x5 at the point x=3. \text { Evaluate the derivative of the function } y = \sqrt [ 5 ] { 2 x ^ { 5 } + 2 x } \text { at the point } x = 3 \text {. } Evaluate the derivative of the function y=52x5+2x​ at the point x=3.

Find the derivative of the function f(x)=arcsec⁡(9x). \text { Find the derivative of the function } f ( x ) = \operatorname { arcsec } ( 9 x ) \text {. } Find the derivative of the function f(x)=arcsec(9x).

Find dydt when x=π7. \text { Find } \frac { d y } { d t } \text { when } x = \frac { \pi } { 7 } \text {. } Find dtdy​ when x=7π​.

Find an equation of the tangent line to the graph of the function (y−6)2=5(x−5)( y - 6 ) ^ { 2 } = 5 ( x - 5 )(y−6)2=5(x−5) at the point (8.20,2.00)( 8.20,2.00 )(8.20,2.00) . The coefficients below are given to two decimal places.

Find dydx by implicit differentiation given that x89+y89=2. \text { Find } \frac { d y } { d x } \text { by implicit differentiation given that } x ^ { \frac { 8 } { 9 } } + y ^ { \frac { 8 } { 9 } } = 2 \text {. } Find dxdy​ by implicit differentiation given that x98​+y98​=2.

Use the Product Rule to differentiate. f(t)=t−3cos⁡tf ( t ) = t ^ { - 3 } \cos tf(t)=t−3cost

Find the derivative of the function f(x)=ex−4ex+4. Simplify your answer. \text { Find the derivative of the function } f ( x ) = \frac { e ^ { x } - 4 } { e ^ { x } + 4 } \text {. Simplify your answer. } Find the derivative of the function f(x)=ex+4ex−4​. Simplify your answer.

Find dydx by implicit differentiation. \text { Find } \frac { d y } { d x } \text { by implicit differentiation. } Find dxdy​ by implicit differentiation. sin⁡x+7cos⁡14y=2\sin x + 7 \cos 14 y = 2sinx+7cos14y=2

Find the derivative of the function h(t)=2sin⁡(arccos⁡t). \text { Find the derivative of the function } h ( t ) = 2 \sin ( \arccos t ) \text {. } Find the derivative of the function h(t)=2sin(arccost).

Graphs and Models

A Preview of Calculus

Extrema on an Interval

Antiderivatives and Indefinite Integration

Slope Fields and Eulers Method

Area of a Region Between Two Curves

Basic Integration Rules

Sequences

Conics and Calculus

Vectors in the Plane

Vector-Valued Functions

Introduction to Functions of Several Variables

Iterated Integrals and Area in the Plane

Vector Fields

Exact First-Order Equations

Filters

$\text { Find the derivative of the function } f ( x ) = - 7 x ^ { 3 } + 4 x ^ { 2 } + 1 \text {. }$

$\text { Find the slope-intercept equation of the line tangent to the graph of } y = e ^ { x } \text { when }$ $x = \ln 3$

Assume that x and y are both differentiable functions of t . Find $\frac { d y } { d t }$ when $x = 49$ and $\frac { d x } { d t } = 17$ for the equation $y = \sqrt { x }$ .

$\text { Find } \frac { d ^ { 2 } y } { d x ^ { 2 } } \text { in terms of } x \text { and } y \text { given that } 3 - 7 x y = 3 x - 7 y$

Find the derivative of the function. $f ( x ) = \frac { 1 } { x ^ { 8 } }$

$\text { Evaluate the derivative of the function } y = \sqrt [ 5 ] { 2 x ^ { 5 } + 2 x } \text { at the point } x = 3 \text {. }$

$\text { Find the derivative of the function } f ( x ) = \operatorname { arcsec } ( 9 x ) \text {. }$

$\text { Find } \frac { d y } { d t } \text { when } x = \frac { \pi } { 7 } \text {. }$

Find an equation of the tangent line to the graph of the function $( y - 6 ) ^ { 2 } = 5 ( x - 5 )$ at the point $( 8.20,2.00 )$ . The coefficients below are given to two decimal places.

$\text { Find } \frac { d y } { d x } \text { by implicit differentiation given that } x ^ { \frac { 8 } { 9 } } + y ^ { \frac { 8 } { 9 } } = 2 \text {. }$

Use the Product Rule to differentiate. $f ( t ) = t ^ { - 3 } \cos t$

$\text { Find the derivative of the function } f ( x ) = \frac { e ^ { x } - 4 } { e ^ { x } + 4 } \text {. Simplify your answer. }$

$\text { Find } \frac { d y } { d x } \text { by implicit differentiation. }$ $\sin x + 7 \cos 14 y = 2$

$\text { Find the derivative of the function } h ( t ) = 2 \sin ( \arccos t ) \text {. }$