Exam 1: Graphs and Models
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
horsepower H required to overcome wind drag on a certain automobile is approximated by where is the speed of the car in miles per hour. Find . Round the numerical values in your answer to five decimal places.
Free
(Multiple Choice)
4.8/5  (43)
(43)
Correct Answer:
D
Determine which type of function would be most appropriate to fit the given data.
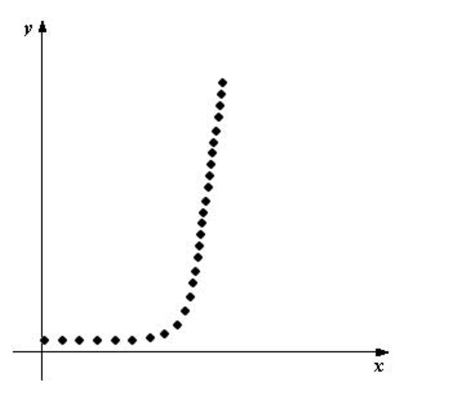
(Multiple Choice)
4.9/5  (39)
(39)
The following ordered pairs represent temperatures in degrees Fahrenheit taken each hour from until 5:00 pm. Let be temperature, and let be time, where corresponds to corresponds to , and so on. Plot the data. Visually find a linear model for the data and find its equation. From the visual linear model that you created, determine which of the models that follow appears to best approximate the data.
(Multiple Choice)
4.8/5  (46)
(46)
Match the graph of the function given below with the graph of its inverse function.
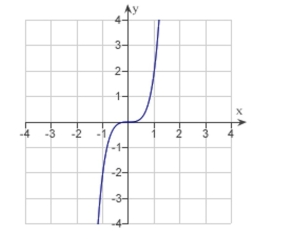
(Multiple Choice)
4.8/5  (35)
(35)
", to write an equation of the line with -intercept: and intercept: .
(Multiple Choice)
4.8/5  (27)
(27)
Each ordered pair gives the exposure index x of a carcinogenic substance and the cancer mortality per 100,000 people in the population. Use the model to approximate if . Round your answer to one decimal place.
(3.50,150.1),(3.58,133.1),(4.42,132.9),(2.26,116.7),(2.36,140.7),(4.85,165.5) (12.65,210.7),(7.42,181.0),(9.35,213.4)
(Multiple Choice)
4.9/5  (38)
(38)
Fine the slope of the line passing through the pair of points.
(Multiple Choice)
4.8/5  (35)
(35)
Write an equation of the line that passes through the given point and is parallel to the given line. Point Line (3,-4) -2x-5y=9
(Multiple Choice)
4.9/5  (36)
(36)
Use the Horizontal Line Test to determine whether the following statement is true or false. The function is one-to-one on its entire domain and therefore has an inverse function.
(True/False)
4.8/5  (35)
(35)
Showing 1 - 20 of 114
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)