Exam 16: Exact First-Order Equations
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Use the electrical circuit differential equation where is the resistance (in ohms), is the capacitance (in farads), is the inductance (in henrys), is the electromotive force (in volts), and is the charge on the capacitor (in coulombs). Find the charge as a function of time for the electrical circuit described. Assume that and .
Free
(Multiple Choice)
4.7/5  (42)
(42)
Correct Answer:
B
Solve the differential equation coefficients.
Free
(Multiple Choice)
4.7/5  (37)
(37)
Correct Answer:
D
Find the first six terms of the power series representing independent solutions of the differential equation .
(Multiple Choice)
4.7/5  (43)
(43)
Find the interval of convergence for the solution of the differential equation
(Multiple Choice)
4.9/5  (32)
(32)
Use Taylor's Theorem to find the first four terms of the series solution of given the initial conditions , and and use it to calculate . Round your answer to three decimal places.
(Multiple Choice)
4.9/5  (30)
(30)
Find the interval of convergence for the solution of the differential equation
(Multiple Choice)
4.9/5  (38)
(38)
Find the series solution of the differential equation conditions and
(Multiple Choice)
4.9/5  (34)
(34)
Use Taylor's Theorem to find the first eight terms of the series solution of given the initial conditions and use it to calculate .
Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (43)
(43)
Find the particular solution of the differential equation for the oscillating motion of an object on the end of a spring. In the equation, is the displacement from equilibrium (positive direction is downward) measured in feet, and is the time in seconds (see figure). The constant is the weight of the object, is the acceleration due to gravity, is the magnitude of the resistance to the motion, is the spring constant from Hooke's Law, is the acceleration imposed on the system, and
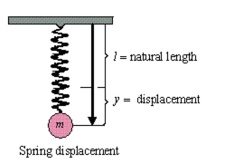
(Multiple Choice)
4.9/5  (36)
(36)
Find the first eight terms of the power series representing independent solutions of the differential equation .
(Multiple Choice)
4.8/5  (36)
(36)
Find the integrating factor of the differential equation a function of x or y alone.
(Multiple Choice)
4.9/5  (35)
(35)
Find the particular solution of the differential equation that satisfies the initial condition
(Multiple Choice)
4.9/5  (36)
(36)
Find the particular solution of the differential equation
that satisfies the initial condition .
(Multiple Choice)
4.8/5  (34)
(34)
Solve the differential equation are solutions of the corresponding homogeneous equation.
(Multiple Choice)
4.7/5  (36)
(36)
Showing 1 - 20 of 45
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)