Exam 7: Area of a Region Between Two Curves
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the given lines.
(i) -axis; (ii) the line
Free
(Multiple Choice)
4.9/5  (41)
(41)
Correct Answer:
A
Find Mx,My , and ( , ) for the lamina of uniform density text bounded by the graphs
Free
(Multiple Choice)
4.9/5  (40)
(40)
Correct Answer:
C
Find the area of the region bounded by the graphs of the algebraic functions. f(x)=-20x g(x)=0
Free
(Multiple Choice)
4.8/5  (35)
(35)
Correct Answer:
A
Find the area of the region bounded by the graphs of the algebraic functions.
(Multiple Choice)
4.8/5  (32)
(32)
Find the area of the region bounded by the graphs of the algebraic functions.
f(x)= g(x)=x-8
(Multiple Choice)
4.7/5  (37)
(37)
Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the x-axis.
(Multiple Choice)
4.8/5  (44)
(44)
Find Mx for the lamina of uniform density bounded by the graphs of the
equations
and .
(Multiple Choice)
4.8/5  (41)
(41)
A rectangular plate of height h feet and base b feet is submerged vertically in a tank of fluid that weighs pounds per cubic foot. The center of the plate is feet below the surface of the fluid. The fluid force on the surface of the plate is given by Find the fluid force on the rectangular plate as shown in the figure given feet and feet. Round your answer to one decimal place.
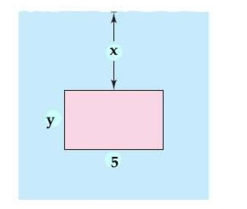
(Multiple Choice)
4.9/5  (33)
(33)
Find the fluid force on the vertical side of the tank, where the dimensions are given in feet. Assume that the tank is full of water. Note: The density of water is 62.4 lbs per cubic foot. 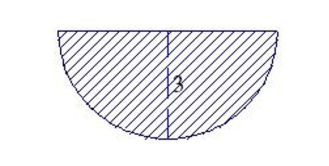
(Multiple Choice)
4.9/5  (30)
(30)
Set up and evaluate the integral that gives the volume of the solid formed by revolving the region bounded by and in the first quadrant about the -axis.
(Multiple Choice)
4.8/5  (40)
(40)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the given lines.
(i) -axis; (ii) the line
(Multiple Choice)
4.9/5  (28)
(28)
Use the disk or the shell method to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the -axis. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (33)
(33)
Find the area of the region bounded by the equations by integrating
(i) with respect to x and
(ii) with respect to y.
x=16- x=y-4
(Multiple Choice)
4.8/5  (34)
(34)
Find the area of the region bounded by the graphs of the equations.
(Multiple Choice)
5.0/5  (34)
(34)
A circular plate of radius r feet is submerged vertically in a tank of fluid that weighs pounds per cubic foot. The center of the circle is feet below the surface of the fluid. The fluid force on the surface of the plate is given by Find the fluid force on the circular plate as shown in the figure given feet and feet. Round your answer to one decimal place.
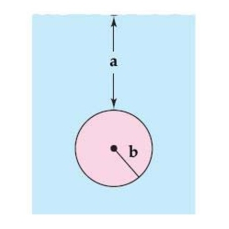
(Multiple Choice)
4.9/5  (43)
(43)
Use the disk or shell method to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the line .
(Multiple Choice)
4.9/5  (39)
(39)
Find the area of the region bounded by the graphs of the function . Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (38)
(38)
Set up and evaluate integrals for finding the moment about the y-axis for the region bounded by the graphs of the equations. (Assume )
(Multiple Choice)
4.7/5  (35)
(35)
Use the shell method to set up and evaluate an integral that gives the volume of the solid generated by revolving the plane region about the y-axis.
(Multiple Choice)
4.9/5  (38)
(38)
Find the buoyant force of a rectangular solid of the given dimensions submerged in water so that the top side is parallel to the surface of the water. The buoyant force is the difference
Between the fluid forces on the top and bottom sides of the solid. Round your answer to two decimal Places. 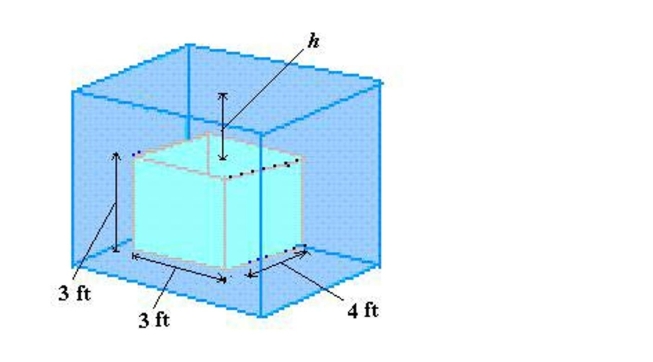
(Multiple Choice)
4.8/5  (33)
(33)
Showing 1 - 20 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)