Exam 2: A Preview of Calculus
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Find the following limit if it exists: . Use when appropriate.
Free
(Multiple Choice)
4.9/5  (31)
(31)
Correct Answer:
D
A sphere has a volume of 4.76 cubic inches. What is the radius of the sphere? Round your answer to four decimal places.
Free
(Multiple Choice)
4.8/5  (32)
(32)
Correct Answer:
A
Complete the table and use the result to estimate the limit. x -0.1 -0.01 -0.001 0.001 0.01 0.1 f(x)
Free
(Multiple Choice)
4.8/5  (44)
(44)
Correct Answer:
C
Determine the following limit. (Hint: Use the graph to calculate the limit.)
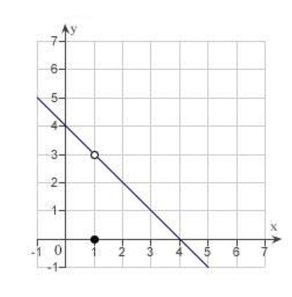
(Multiple Choice)
4.7/5  (34)
(34)
Decide whether the following problem can be solved using precalculus, or whether calculus is required. If the problem can be solved using precalculus, solve it. If the Problem seems to require calculus, use a graphical or numerical approach to estimate the Solution.mFind the distance traveled in 16 seconds by an object traveling at a constant velocity of 20 feet Per second.
(Multiple Choice)
4.9/5  (47)
(47)
the left and from the right by completing the tables below.
x -3.5 -3.1 -3.01 -3.001 f(x)
x -2.999 -2.99 -2.9 -2.5 f(x)
(Multiple Choice)
4.8/5  (40)
(40)
Find all the vertical asymptotes (if any) of the graph of the function
(Multiple Choice)
4.8/5  (25)
(25)
Use the graph as shown to determine the following limits, and discuss the continuity of the function at
(i)
(ii)
(iii)
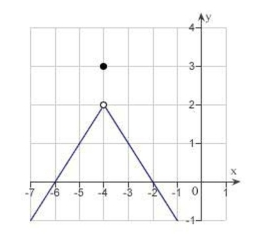
(Multiple Choice)
5.0/5  (28)
(28)
Estimate the slope of the tangent line of at . Round your answer to four decimal places.
(Multiple Choice)
4.8/5  (31)
(31)
Showing 1 - 20 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)