Exam 16: Series and Taylor Polynomials Web
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
Suppose the ratio of alligators to pythons in a marshland from 2001 to 2008 can be approximated by the model where is the year, with corresponding to In 2006, the total number of alligators and pythons in the marsh was about 900. In that year, how many were pythons?
(Multiple Choice)
4.8/5  (42)
(42)
The annual sales (in millions of dollars) for a certain company from 2001 to 2006 can be approximated by the model where represents the year, with corresponding to 2001. Find the total sales from 2001 to 2004. Round to the nearest million.
(Multiple Choice)
4.8/5  (37)
(37)
Determine whether the sequence is arithmetic. If so, find the common difference. (Assume that n begins with 1.)
(Multiple Choice)
4.8/5  (43)
(43)
Use Newton's Method to approximate . Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (30)
(30)
Determine whether the sequence is geometric. If so, find the common ratio. 5, 7, 9, 11, ...
(Multiple Choice)
4.9/5  (35)
(35)
Use Newton's Method to find the point on the graph of that is closest to the point . Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (42)
(42)
Use Newton's Method to approximate the x-value of the indicated point intersection of the two graphs accurate to three decimal places. f(x)=2x+1 g(x)= 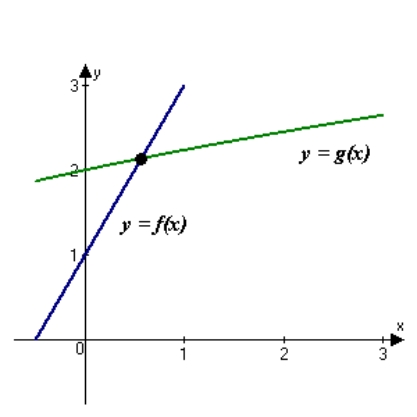
(Multiple Choice)
4.8/5  (33)
(33)
Use the fourth-degree Taylor polynomial centered at c = 2 for the function to approximate . Round your answer to nearest ten thousandth.
(Multiple Choice)
4.8/5  (39)
(39)
Write an expression for the nth term of the sequence 2, 8, 26, 80, ....
(Multiple Choice)
4.8/5  (42)
(42)
Determine whether the sequence is geometric. If so, find the common ratio. 1, -3, 9, -27, ...
(Multiple Choice)
5.0/5  (40)
(40)
Consider a job offer with a starting salary of $43,200 and a given annual raise of $2175. Determine the total compensation from the company through seven full years of employment.
(Multiple Choice)
4.9/5  (42)
(42)
Match the arithmetic sequence with its graph from the choices below.
(Multiple Choice)
4.9/5  (39)
(39)
Find the power series for the function using the power series for .
(Multiple Choice)
4.9/5  (37)
(37)
The annual spending by tourists in a resort city is 200 million dollars. Approximately 75% of that revenue is again spent in the resort city, and of that amount approximately 75% is again spent in the resort city. If this pattern continues, write the geometric series that gives the total amount of spending generated by the 200 million dollars (including the initial outlay of 200 million dollars) and find the sum of the series.
(Multiple Choice)
4.9/5  (37)
(37)
Showing 21 - 40 of 127
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)