Exam 16: Series and Taylor Polynomials Web
Exam 1: Fundamental Concepts of Algebra119 Questions
Exam 2: Equations and Inequalities94 Questions
Exam 3: Functions and Graphs96 Questions
Exam 4: Polynomial and Rational Functions105 Questions
Exam 5: Exponential and Logarithmic Functions94 Questions
Exam 6: Systems of Equations and Inequalities96 Questions
Exam 7: Matrices and Determinants94 Questions
Exam 8: Limits and Derivatives77 Questions
Exam 9: Applications of the Derivative83 Questions
Exam 10: Further Applications of the Derivative83 Questions
Exam 11: Derivatives of Exponential and Logarithmic Functions121 Questions
Exam 12: Integration and Its Applications74 Questions
Exam 13: Techniques of Integration50 Questions
Exam 14: Functions of Several Variables92 Questions
Exam 15: Trigonometric Functions Web60 Questions
Exam 16: Series and Taylor Polynomials Web127 Questions
Exam 17: Probability Web89 Questions
Select questions type
Differentiate the series for to find the power series for the function .
(Multiple Choice)
4.8/5  (38)
(38)
Write an expression for the apparent nth term of the sequence. (Assume that n begins with 1.) 9, 12, 15, 18, 21
(Multiple Choice)
4.7/5  (42)
(42)
The value for which Newton's method fails for the function below is shown in the graph. Give the reason why the method fails. 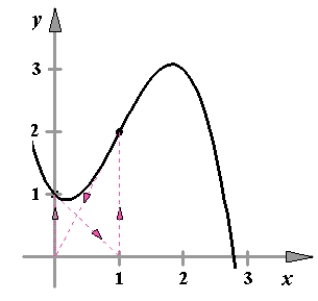
(Multiple Choice)
4.8/5  (36)
(36)
Bouncing Ball. A ball dropped from a height of 35 feet bounces to of its former height with each bounce. Find the total vertical distance that the ball travels.
(Multiple Choice)
4.8/5  (29)
(29)
Determine the convergence or divergence of the sequence . If the sequence converges, use a symbolic algebra utility to find its limit.
(Multiple Choice)
4.9/5  (40)
(40)
You are in a boat 2 miles from the nearest point on the coast (see figure). You are to go to a point Q, which is 3 miles down the coast and 1 mile inland. You can row at 4 miles per hour and walk at 5 miles per hour. Toward what point on the coast should you row in order to reach point Q in the least time? Round your answer to three decimal places. 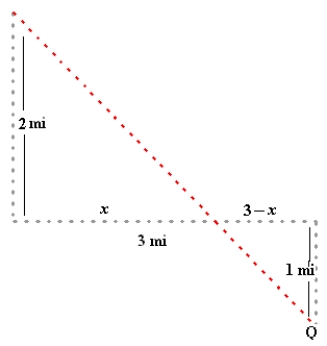
(Multiple Choice)
4.8/5  (34)
(34)
A factory is polluting a river such that at every mile down river from the factory an environmental expert finds 20% less pollutant than at the preceding mile. If the pollutant's concentration is 700 ppm (parts per million) at the factory, what is its concentration 15 miles down river?
(Multiple Choice)
4.9/5  (34)
(34)
Consider the sequence (An) whose nth term is given by An where P is the principal, An is the amount of compound interest after n months, and r is the annual percentage rate. Write the first four terms of the sequence for P = 8,000 and r = 0.04. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (37)
(37)
You accept a job that pays a salary of 50,000 the first year. During the next 39 years, you will receive a 4% raise each year. What would be your total compensation over the 40-year period? Round your answer to the nearest integer.
(Multiple Choice)
4.9/5  (41)
(41)
Determine the convergence or divergence of the series . Use a symbolic algebra utility to verify your result.
(Multiple Choice)
4.8/5  (34)
(34)
Determine whether the sequence is arithmetic. If so, find the common difference. 3, 9, 27, 81, 243
(Multiple Choice)
5.0/5  (36)
(36)
Apply Taylor's Theorem to find the power series centered at for the function .
(Multiple Choice)
4.8/5  (36)
(36)
Use a graphing utility to graph the first 10 terms of the sequence.
(Multiple Choice)
4.7/5  (34)
(34)
Find the Taylor polynomials (centred at zero) of degree (a) 1, (b) 2, (c) 3, and (d) 4.
(Multiple Choice)
4.8/5  (41)
(41)
A deposit of $2000 is made in an account that earns 6% interest compounded monthly. The balance in the account after n months is given by Find the balance in the account after 11 years by finding the 132th term of the sequence. Round to the nearest penny.
(Multiple Choice)
4.9/5  (43)
(43)
The ordering and transportation cost C of the components used in manufacturing a product is given by where C is measured in thousands of dollars and x is the order size in hundreds. Find the order size that minimizes the cost. Round your answer to the nearest unit.
(Multiple Choice)
5.0/5  (40)
(40)
Write an expression for the most apparent nth term of the sequence. (Assume that begins with 1.)
(Multiple Choice)
4.9/5  (32)
(32)
Showing 61 - 80 of 127
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)