Exam 14: Introduction to Multiple Regression
Exam 1: Defining and Collecting Data207 Questions
Exam 2: Organizing and Visualizing Variables213 Questions
Exam 3: Numerical Descriptive Measures167 Questions
Exam 4: Basic Probability171 Questions
Exam 5: Discrete Probability Distributions217 Questions
Exam 6: The Normal Distributions and Other Continuous Distributions189 Questions
Exam 7: Sampling Distributions135 Questions
Exam 8: Confidence Interval Estimation189 Questions
Exam 9: Fundamentals of Hypothesis Testing: One-Sample Tests187 Questions
Exam 10: Two-Sample Tests208 Questions
Exam 11: Analysis of Variance216 Questions
Exam 12: Chi-Square and Nonparametric Tests178 Questions
Exam 13: Simple Linear Regression214 Questions
Exam 14: Introduction to Multiple Regression336 Questions
Exam 15: Multiple Regression Model Building99 Questions
Exam 16: Time-Series Forecasting173 Questions
Exam 17: Business Analytics115 Questions
Exam 18: A Roadmap for Analyzing Data329 Questions
Exam 19: Statistical Applications in Quality Management Online162 Questions
Exam 20: Decision Making Online129 Questions
Exam 21: Understanding Statistics: Descriptive and Inferential Techniques39 Questions
Select questions type
SCENARIO 14-4 A real estate builder wishes to determine how house size (House)is influenced by family income (Income)and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below: 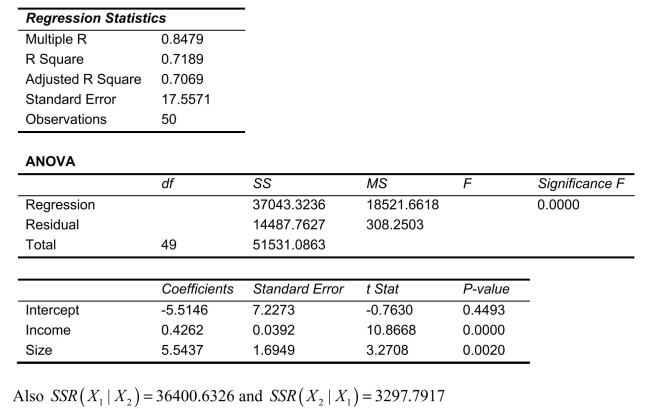 -Referring to Scenario 14-4, what is the predicted house size (in hundreds of square feet)for an individual earning an annual income of $40,000 and having a family size of 4?
-Referring to Scenario 14-4, what is the predicted house size (in hundreds of square feet)for an individual earning an annual income of $40,000 and having a family size of 4?
(Short Answer)
4.9/5  (39)
(39)
SCENARIO 14-7 The department head of the accounting department wanted to see if she could predict the GPA of students using the number of course units and total SAT scores of each.She takes a sample of students and generates the following Microsoft Excel output: 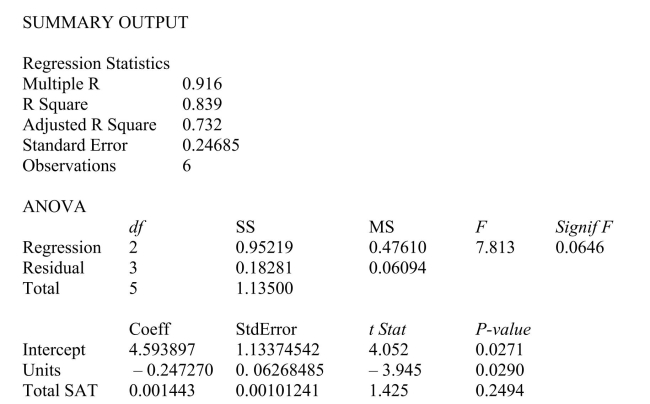 -Referring to Scenario 14-7, the department head wants to use a t test to test for the significance of the coefficient of
-Referring to Scenario 14-7, the department head wants to use a t test to test for the significance of the coefficient of 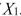 The value of the test statistic is ________.
The value of the test statistic is ________.
(Short Answer)
4.8/5  (37)
(37)
SCENARIO 14-8 A financial analyst wanted to examine the relationship between salary (in $1,000)and 2 variables: age 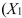 = Age)and experience in the field
= Age)and experience in the field 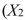 = Exper).He took a sample of 20 employees and obtained the following Microsoft Excel output:
= Exper).He took a sample of 20 employees and obtained the following Microsoft Excel output: 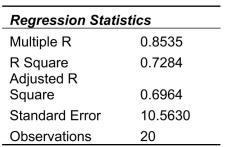
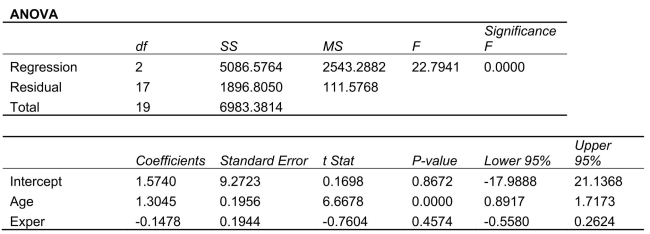 Also, the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848.
-Referring to Scenario 14-8, the predicted salary (in $1,000)for a 35-year-old person with 10 years of experience is ________.
Also, the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848.
-Referring to Scenario 14-8, the predicted salary (in $1,000)for a 35-year-old person with 10 years of experience is ________.
(Short Answer)
4.8/5  (37)
(37)
SCENARIO 14-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending)of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, 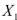 = Salaries and
= Salaries and 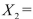 Spending:
Spending: 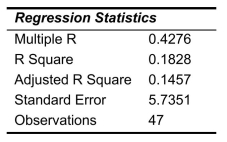
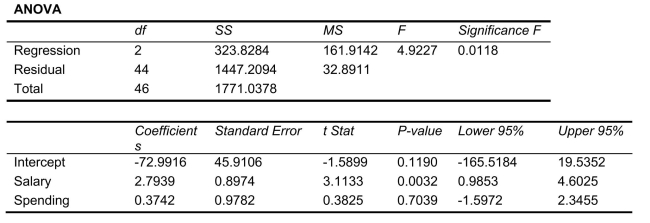 -Referring to Scenario 14-15, you can conclude definitively that instructional spending per pupil individually has no impact on the mean percentage of students passing the proficiency test, considering the effect of mean teacher salary, at a 1% level of significance based solely on but not actually computing the 99% the confidence interval estimate for
-Referring to Scenario 14-15, you can conclude definitively that instructional spending per pupil individually has no impact on the mean percentage of students passing the proficiency test, considering the effect of mean teacher salary, at a 1% level of significance based solely on but not actually computing the 99% the confidence interval estimate for 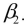
(True/False)
4.8/5  (30)
(30)
SCENARIO 14-8 A financial analyst wanted to examine the relationship between salary (in $1,000)and 2 variables: age 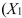 = Age)and experience in the field
= Age)and experience in the field 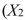 = Exper).He took a sample of 20 employees and obtained the following Microsoft Excel output:
= Exper).He took a sample of 20 employees and obtained the following Microsoft Excel output: 
 Also, the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848.
-Referring to Scenario 14-8, the coefficient of partial determination
Also, the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848.
-Referring to Scenario 14-8, the coefficient of partial determination 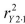 is ____.
is ____.
(Short Answer)
4.9/5  (33)
(33)
SCENARIO 14-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending)of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, 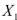 = Salaries and
= Salaries and 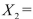 Spending:
Spending: 
 -Referring to Scenario 14-15, what is the standard error of estimate?
-Referring to Scenario 14-15, what is the standard error of estimate?
(Short Answer)
4.8/5  (34)
(34)
SCENARIO 14-8 A financial analyst wanted to examine the relationship between salary (in $1,000)and 2 variables: age 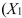 = Age)and experience in the field
= Age)and experience in the field 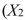 = Exper).He took a sample of 20 employees and obtained the following Microsoft Excel output:
= Exper).He took a sample of 20 employees and obtained the following Microsoft Excel output: 
 Also, the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848.
-Referring to Scenario 14-8, the partial F test for
Also, the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848.
-Referring to Scenario 14-8, the partial F test for 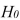 : Variable
: Variable 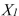 does not significantly improve the model after variable
does not significantly improve the model after variable 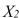 has been included
has been included 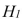 : Variable
: Variable 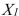 significantly improves the model after variable
significantly improves the model after variable 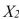 has been included has ____ and ____ degrees of freedom.
has been included has ____ and ____ degrees of freedom.
(Short Answer)
4.7/5  (29)
(29)
SCENARIO 14-17 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy)and the independent variables are the age of the worker (Age)and a dummy variable for management position (Manager: 1 = yes, 0 = no). The results of the regression analysis are given below: 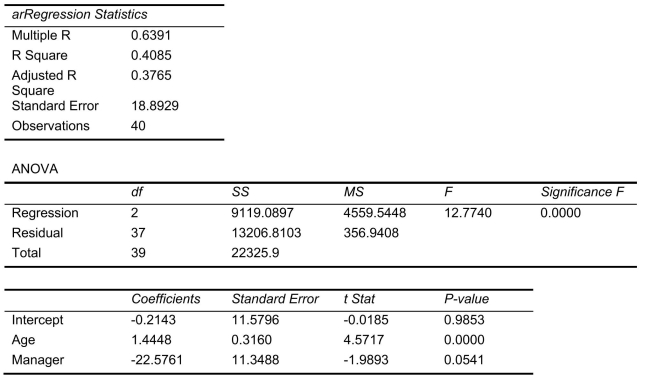 -Referring to Scenario 14-17, the null hypothesis should be rejected at a 10% level of significance when testing whether age has any effect on the number of weeks a worker is unemployed due to a layoff while holding constant the effect of the other independent variable.
-Referring to Scenario 14-17, the null hypothesis should be rejected at a 10% level of significance when testing whether age has any effect on the number of weeks a worker is unemployed due to a layoff while holding constant the effect of the other independent variable.
(True/False)
4.8/5  (37)
(37)
SCENARIO 14-4 A real estate builder wishes to determine how house size (House)is influenced by family income (Income)and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below:  -Referring to Scenario 14-4, what annual income (in thousands of dollars)would an individual with a family size of 9 need to attain a predicted 5,000 square foot home (House = 50)?
-Referring to Scenario 14-4, what annual income (in thousands of dollars)would an individual with a family size of 9 need to attain a predicted 5,000 square foot home (House = 50)?
(Short Answer)
4.8/5  (39)
(39)
SCENARIO 14-4 A real estate builder wishes to determine how house size (House)is influenced by family income (Income)and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below:  -Referring to Scenario 14-4, suppose the builder wants to test whether the coefficient on Size is significantly different from 0.What is the value of the relevant t-statistic?
-Referring to Scenario 14-4, suppose the builder wants to test whether the coefficient on Size is significantly different from 0.What is the value of the relevant t-statistic?
(Multiple Choice)
4.8/5  (42)
(42)
SCENARIO 14-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending)of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, 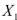 = Salaries and
= Salaries and 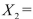 Spending:
Spending: 
 -Referring to Scenario 14-15, the alternative hypothesis
-Referring to Scenario 14-15, the alternative hypothesis 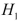 : At least one of
: At least one of 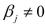 for j = 1, 2 implies that percentage of students passing the proficiency test is related to both of the explanatory variables.
for j = 1, 2 implies that percentage of students passing the proficiency test is related to both of the explanatory variables.
(True/False)
4.9/5  (35)
(35)
SCENARIO 14-17 Given below are results from the regression analysis where the dependent variable is the number of weeks a worker is unemployed due to a layoff (Unemploy)and the independent variables are the age of the worker (Age)and a dummy variable for management position (Manager: 1 = yes, 0 = no). The results of the regression analysis are given below:  -Referring to Scenario 14-17, which of the following is the correct alternative hypothesis to test whether age has any effect on the number of weeks a worker is unemployed due to a layoff while holding constant the effect of the other independent variable?
-Referring to Scenario 14-17, which of the following is the correct alternative hypothesis to test whether age has any effect on the number of weeks a worker is unemployed due to a layoff while holding constant the effect of the other independent variable?
(Multiple Choice)
4.9/5  (36)
(36)
SCENARIO 14-10 You worked as an intern at We Always Win Car Insurance Company last summer.You notice that individual car insurance premiums depend very much on the age of the individual and the number of traffic tickets received by the individual.You performed a regression analysis in EXCEL and obtained the following partial information: 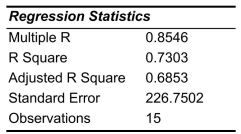
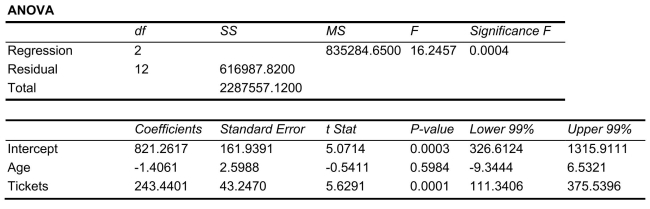 -Referring to Scenario 14-10, to test the significance of the multiple regression model, the value of the test statistic is ______.
-Referring to Scenario 14-10, to test the significance of the multiple regression model, the value of the test statistic is ______.
(Short Answer)
4.9/5  (38)
(38)
SCENARIO 14-6 One of the most common questions of prospective house buyers pertains to the cost of heating in dollars (Y).To provide its customers with information on that matter, a large real estate firm used the following 2 variables to predict heating costs: the daily minimum outside temperature in degrees of Fahrenheit 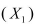 and the amount of insulation in inches
and the amount of insulation in inches 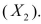 Given below is EXCEL output of the regression model.
Given below is EXCEL output of the regression model. 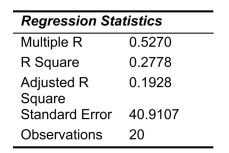
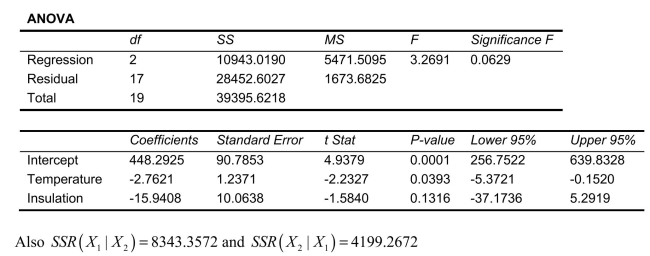 -Referring to Scenario 14-6, the estimated value of the regression parameter
-Referring to Scenario 14-6, the estimated value of the regression parameter 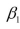 in means that
in means that
(Multiple Choice)
4.8/5  (38)
(38)
SCENARIO 14-4 A real estate builder wishes to determine how house size (House)is influenced by family income (Income)and family size (Size).House size is measured in hundreds of square feet and income is measured in thousands of dollars.The builder randomly selected 50 families and ran the multiple regression.Partial Microsoft Excel output is provided below:  -Referring to Scenario 14-4, when the builder used a simple linear regression model with house size (House)as the dependent variable and family size (Size)as the independent variable, he obtained an r2 value of 1.25%.What additional percentage of the total variation in house size has been explained by including income in the multiple regression?
-Referring to Scenario 14-4, when the builder used a simple linear regression model with house size (House)as the dependent variable and family size (Size)as the independent variable, he obtained an r2 value of 1.25%.What additional percentage of the total variation in house size has been explained by including income in the multiple regression?
(Multiple Choice)
4.8/5  (37)
(37)
SCENARIO 14-8 A financial analyst wanted to examine the relationship between salary (in $1,000)and 2 variables: age 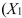 = Age)and experience in the field
= Age)and experience in the field 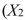 = Exper).He took a sample of 20 employees and obtained the following Microsoft Excel output:
= Exper).He took a sample of 20 employees and obtained the following Microsoft Excel output: 
 Also, the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848.
-Referring to Scenario 14-8, ____% of the variation in salary can be explained by the variation in age while holding experience constant.
Also, the sum of squares due to the regression for the model that includes only Age is 5022.0654 while the sum of squares due to the regression for the model that includes only Exper is 125.9848.
-Referring to Scenario 14-8, ____% of the variation in salary can be explained by the variation in age while holding experience constant.
(Short Answer)
4.8/5  (43)
(43)
In a particular model, the sum of the squared residuals was 847.If the model had 5 independent variables, and the data set contained 40 points, the value of the standard error of the estimate is 24.912.
(True/False)
4.8/5  (26)
(26)
SCENARIO 14-19 The marketing manager for a nationally franchised lawn service company would like to study the characteristics that differentiate home owners who do and do not have a lawn service.A random sample of 30 home owners located in a suburban area near a large city was selected; 11 did not have a lawn service (code 0)and 19 had a lawn service (code 1).Additional information available concerning these 30 home owners includes family income (Income, in thousands of dollars)and lawn size (Lawn Size, in thousands of square feet). The PHStat output is given below: 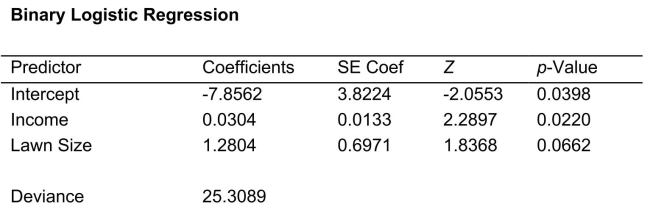 -Referring to Scenario 14-19, there is not enough evidence to conclude that the model is not a good-fitting model at a 0.05 level of significance.
-Referring to Scenario 14-19, there is not enough evidence to conclude that the model is not a good-fitting model at a 0.05 level of significance.
(True/False)
4.8/5  (29)
(29)
SCENARIO 14-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending)of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, 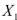 = Salaries and
= Salaries and 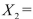 Spending:
Spending: 
 -Referring to Scenario 14-15, the null hypothesis
-Referring to Scenario 14-15, the null hypothesis 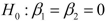 implies that percentage of students passing the proficiency test is not affected by one of the explanatory variables.
implies that percentage of students passing the proficiency test is not affected by one of the explanatory variables.
(True/False)
4.8/5  (38)
(38)
SCENARIO 14-15 The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test.She obtained the data on percentage of students passing the proficiency test (% Passing), mean teacher salary in thousands of dollars (Salaries), and instructional spending per pupil in thousands of dollars (Spending)of 47 schools in the state. Following is the multiple regression output with Y = % Passing as the dependent variable, 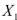 = Salaries and
= Salaries and 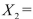 Spending:
Spending: 
 -Referring to Scenario 14-15, you can conclude definitively that instructional spending per pupil individually has no impact on the mean percentage of students passing the proficiency test, considering the effect of mean teacher salary, at a 10% level of significance based solely on but not actually computing the 90% confidence interval estimate for
-Referring to Scenario 14-15, you can conclude definitively that instructional spending per pupil individually has no impact on the mean percentage of students passing the proficiency test, considering the effect of mean teacher salary, at a 10% level of significance based solely on but not actually computing the 90% confidence interval estimate for 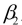
(True/False)
4.7/5  (44)
(44)
Showing 201 - 220 of 336
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)