Question 1

If all the squared terms in a quadratic function have a negative coefficient and there are no cross-product terms, then the function is a _____ function.

Accepted Answer

A)  convex quadratic 
B)  nonlinear objective 
C)  concave quadratic 
D)  negative elliptical 
A)  convex quadratic 
B)  nonlinear objective 
C)  concave quadratic 
D)  negative elliptical

Question 2

One of the ways to formulate the Markowitz model is to:

Accepted Answer

A)  maximize the variance of the portfolio subject to a constraint on the expected return of the portfolio. 
B)  minimize the expected return of the portfolio subject to a constraint on variance. 
C)  minimize the variance of the portfolio subject to a constraint on the expected return of the portfolio. 
D)  minimize the expected return of the portfolio with no constraint on variance. 
A)  maximize the variance of the portfolio subject to a constraint on the expected return of the portfolio. 
B)  minimize the expected return of the portfolio subject to a constraint on variance. 
C)  minimize the variance of the portfolio subject to a constraint on the expected return of the portfolio. 
D)  minimize the expected return of the portfolio with no constraint on variance.

Question 3

A global minimum

Accepted Answer

A)  is also a local maximum. 
B)  need not be a local maximum, but vice versa is true. 
C)  is also a local minimum. 
D)  need not be local minimum, but vice versa is true. 
A)  is also a local maximum. 
B)  need not be a local maximum, but vice versa is true. 
C)  is also a local minimum. 
D)  need not be local minimum, but vice versa is true.

Question 4

A feasible solution is _____ if there are no other feasible points with a better objective function value in the entire feasible region.

Accepted Answer

A)  infeasible 
B)  unbounded 
C)  nonlinear 
D)  a global optimum 
A)  infeasible 
B)  unbounded 
C)  nonlinear 
D)  a global optimum

Question 5

A feasible solution is _____ if there are no other feasible points with a smaller objective function value in the entire feasible region.

Accepted Answer

A)  a global minimum 
B)  not a local maximum 
C)  not a local minimum 
D)  bowl-shaped 
A)  a global minimum 
B)  not a local maximum 
C)  not a local minimum 
D)  bowl-shaped

Question 6

The _____ of a solution is a mathematical concept that refers to the set of points within a relatively close proximity of the solution.

Accepted Answer

A)  objective function contour 
B)  neighborhood 
C)  regression equation 
D)  Lagrangian multiplier 
A)  objective function contour 
B)  neighborhood 
C)  regression equation 
D)  Lagrangian multiplier

Question 7

A(n) _____ is a set of points defining the minimum possible risk for a set of return values.

Accepted Answer

A)  Contour 
B)  Efficient frontier 
C)  Unity constraint 
D)  Reduced gradient 
A)  Contour 
B)  Efficient frontier 
C)  Unity constraint 
D)  Reduced gradient

Question 8

Jim is trying to solve a problem where the point A should be within the radius of 15cms from points B, C, D, E, and F. The decision variables are defined as below.
X = horizontal coordinate of point A
Y = vertical coordinate of point A
The data on the distances is given below:
   
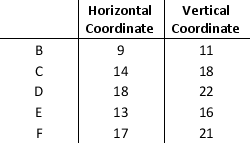Formulate and solve a model that minimizes the maximum distance from point A to each of the points B, C, D, E, and F. Round all your answers to three decimal places.

Accepted Answer

Let X = horizontal coordinate of point A

Question 9

The portfolio variance is the:

Accepted Answer

A)  sum of the squares of the deviations from the mean value under each scenario. 
B)  average of the sum of the squares of the deviations from the mean value under each investment scenario. 
C)  average of the product of the squares of the deviations from the mean value under each scenario. 
D)  average of the sum of the deviations from the mean value under each investment scenario. 
A)  sum of the squares of the deviations from the mean value under each scenario. 
B)  average of the sum of the squares of the deviations from the mean value under each investment scenario. 
C)  average of the product of the squares of the deviations from the mean value under each scenario. 
D)  average of the sum of the deviations from the mean value under each investment scenario.

Question 10

A _____ is the shadow price of a binding simple lower or upper bound on the decision variable.

Accepted Answer

A)  reduced gradient 
B)  binding constraint 
C)  binary variable 
D)  local optimum 
A)  reduced gradient 
B)  binding constraint 
C)  binary variable 
D)  local optimum

Question 11

Consider the EOQ model for multiple products that are independent except for a budget restriction. The following model describes this situation:
Let Dk = annual demand for product k
Ck = unit cost of product k
Sk = cost per order placed for product k
i = inventory carrying charge as a percentage of the cost per unit
B = the maximum amount of investment in goods
N = number of products
The decision variables are Qk, the amount of product k to order. The model is:
 
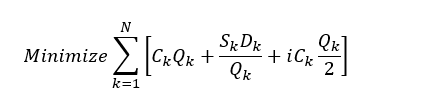s.t.

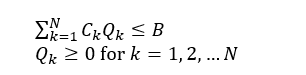a. Set up a spreadsheet model and for the following data:
   
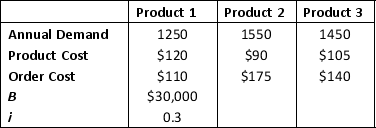b. Solve the problem using Excel Solver. (Hint: For Solver to find a solution, you need to start with decision variable values that are greater than 0.)

Accepted Answer

a.
 @#IMG-DLM& 
b. The optimal solution

Question 12

An Electrical Company has two manufacturing plants. The cost in dollars of producing an Amplifier at each of the two plants is given below. The cost of producing Q1 Amplifiers at first plant is:
65Q₁ + 4Q₁²+ 90
and the cost of producing Q₂ Amplifiers at the second plant is
20Q₂ + 2Q₂²+ 120
The company needs to manufacture at least 60 Amplifiers to meet the received orders. How many Amplifiers should be produced at each of the plant to minimize the total production cost? Round the answers to two decimal places and the total cost to the nearest dollar value.

Accepted Answer

If Q₁ and Q₂ are the number of units of

Question 13

Develop a model that minimizes semivariance for the data given below with a required return of 15 percent. Define a variable ds for each scenario and let ds≥R-Rs with ds ≥ 0. Then make the objective function: Min 14s=14ds2.
   
Solve the model you developed with a required expected return of at least 15 percent.

Accepted Answer

Let:
LG = proportion of portfolio invest

Question 14

A portfolio optimization model used to construct a portfolio that minimizes risk subject to a constraint requiring a minimum level of return is known as_____.

Accepted Answer

A)  capital budgeting pricing model 
B)  market share optimization model 
C)  Hauck maximum variance portfolio model 
D)  Markowitz mean-variance portfolio model 
A)  capital budgeting pricing model 
B)  market share optimization model 
C)  Hauck maximum variance portfolio model 
D)  Markowitz mean-variance portfolio model

Question 15

Consider the following data on the returns from bonds:
   Develop and solve the Markowitz portfolio model using a required expected return of at least 15 percent. Assume that the 8 scenarios are equally likely to occur. Use this model to construct an efficient frontier by varying the expected return from 2 to 18 percent in increment of 2 percent and solving for the variance. Round all your answers to three decimal places.

Accepted Answer

a. Let X = the fraction of the

Question 16

Which of the following conclusions can be drawn from the below figure using the Bass forecasting model? (Note: Bass forecasting model is given by: Ft = (p + q[Ct - ₁ /m]) (m - Ct - ₁),
Where m = the number of people estimated to eventually adopt the new product,
Ct - ₁ = the number of people who have adopted the product through time t - 1,
Q = the coefficient of imitation, and
P = the coefficient of innovation.)

Accepted Answer

A)  q  p 
C)  m  m 
A)  q  p 
C)  m  m

Question 17

Solving nonlinear problems with local optimal solutions is performed using _____, in Excel Solver, which is based on more classical optimization techniques.

Accepted Answer

A)  Goal Seeker 
B)  Linear Regression 
C)  GRG Nonlinear 
D)  Simplex LP 
A)  Goal Seeker 
B)  Linear Regression 
C)  GRG Nonlinear 
D)  Simplex LP

Question 18

A feasible solution is a local minimum if there are no other feasible solutions with a:

Accepted Answer

A)  smaller objective function value in the immediate neighborhood. 
B)  same objective function value in the immediate neighborhood. 
C)  set of points defining the minimum possible risk in the entire feasible region. 
D)  same objective function value in the entire feasible region. 
A)  smaller objective function value in the immediate neighborhood. 
B)  same objective function value in the immediate neighborhood. 
C)  set of points defining the minimum possible risk in the entire feasible region. 
D)  same objective function value in the entire feasible region.

Question 19

Excel Solver's _____ is based on a method that searches for an optimal solution by iteratively adjusting a population of candidate solutions.

Accepted Answer

A)  Evolutionary Solver 
B)  Goal Seeker 
C)  Simplex LP 
D)  GRG Nonlinear 
A)  Evolutionary Solver 
B)  Goal Seeker 
C)  Simplex LP 
D)  GRG Nonlinear

Question 20

Consider the data on investment made in four types of funds and returns from S&P 500.
   a. Develop an optimization model that will give the fraction of the portfolio to invest in each of the funds so that the return of the resulting portfolio matches as closely as possible the return of the S&P 500 Index. (Hint: Minimize the sum of the squared deviations between the portfolio's return and the S&P 500 Index return for each year in the data set.)
b. Solve the model developed in part a.

Accepted Answer

a. Let
LG = proportion of portfolio inve

If all the squared terms in a quadratic function have a negative coefficient and there are no cross-product terms, then the function is a _____ function.

One of the ways to formulate the Markowitz model is to:

A global minimum

A feasible solution is _____ if there are no other feasible points with a better objective function value in the entire feasible region.

A feasible solution is _____ if there are no other feasible points with a smaller objective function value in the entire feasible region.

The _____ of a solution is a mathematical concept that refers to the set of points within a relatively close proximity of the solution.

A(n) _____ is a set of points defining the minimum possible risk for a set of return values.

The portfolio variance is the:

A _____ is the shadow price of a binding simple lower or upper bound on the decision variable.

A portfolio optimization model used to construct a portfolio that minimizes risk subject to a constraint requiring a minimum level of return is known as_____.

Solving nonlinear problems with local optimal solutions is performed using _____, in Excel Solver, which is based on more classical optimization techniques.

A feasible solution is a local minimum if there are no other feasible solutions with a:

Excel Solver's _____ is based on a method that searches for an optimal solution by iteratively adjusting a population of candidate solutions.

Introduction

Descriptive Statistics

Data Visualization

Linear Regression

Time Series Analysis and Forecasting

Data Mining

Spreadsheet Models

Linear Optimization Models

Integer Linear Optimization Models

Monte Carlo Simulation

Decision Analysis

Filters

Exam 10: Nonlinear Optimization Models

If all the squared terms in a quadratic function have a negative coefficient and there are no cross-product terms, then the function is a _____ function.

One of the ways to formulate the Markowitz model is to:

A global minimum

A feasible solution is _____ if there are no other feasible points with a better objective function value in the entire feasible region.

A feasible solution is _____ if there are no other feasible points with a smaller objective function value in the entire feasible region.

The _____ of a solution is a mathematical concept that refers to the set of points within a relatively close proximity of the solution.

A(n) _____ is a set of points defining the minimum possible risk for a set of return values.

The portfolio variance is the:

A _____ is the shadow price of a binding simple lower or upper bound on the decision variable.

A portfolio optimization model used to construct a portfolio that minimizes risk subject to a constraint requiring a minimum level of return is known as_____.

Solving nonlinear problems with local optimal solutions is performed using _____, in Excel Solver, which is based on more classical optimization techniques.

A feasible solution is a local minimum if there are no other feasible solutions with a:

Excel Solver's _____ is based on a method that searches for an optimal solution by iteratively adjusting a population of candidate solutions.

Introduction

Descriptive Statistics

Data Visualization

Linear Regression

Time Series Analysis and Forecasting

Data Mining

Spreadsheet Models

Linear Optimization Models

Integer Linear Optimization Models

Monte Carlo Simulation

Decision Analysis

Filters