Exam 27: Quantifying Uncertainty

The theoretical probability and the experimental probability of an event will be the same.

An experimental rocket will be launched. The launch has an 89% probability of success. With a table of randomly selected digits, what would be an efficient code for success and an efficient code for failure for simulating the launch?

Experiment: Toss four dishonest coins-penny, nickel, dime, quarter-with P(H) = 0.6 for each coin. A computer produced the table below for a simulation of the whole experiment 8000 times. 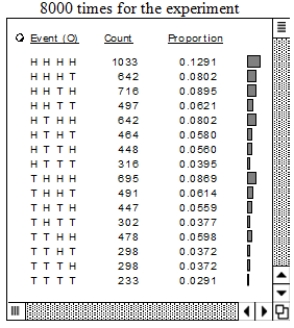A) In the HHHH line (the first line in the body of the table), how did the computer calculate to get 0.1291? B) What is the probability of at least one tail (T), according to this simulation?

A bag has only blue balls and green balls. The experiment is to draw one ball from the bag without looking. What does it mean to say, "The probability of getting a green ball is 70%"?

A) The theoretical probability of getting red for the spinner below isـــــــــــــــــــــــــــــــــــــــــــــــ. (The spinner is a regular hexagon.) 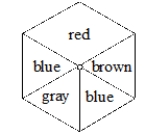B) What does your answer in part A mean? C) Tell how you would find the experimental probability for getting red for the spinner above if you wished to check your theoretical probability.

Fix the following statement so that it clearly describes a probabilistic situation. Jane Smith probably had unusually bad luck last Friday.

Design an experiment based on drawing balls from a bag that would allow for the simulation of a success (getting well) for a sick person undergoing a treatment, with probability of success 0.6.

In an experiment with four outcomes, P, Q, R, and S, the probability of P is $\frac { 1 } { 3 }$ , the probability of Q is $\frac { 1 } { 2 }$ , and the probabilities of R and S are equal to each other. What is the probability of S? A) $\frac { 1 } { 12 }$ B) $\frac { 1 } { 6 }$ C) $\frac { 3 } { 10 }$ D) $\frac { 5 } { 6 }$

You give a child the choice of drawing from two bags of balls. The child wins if he/she draws a red ball. Bag 1 has four red balls and seven green balls; bag 2 has two red balls and three green balls. Which bag gives the child a better chance of winning (or are the chances the same)? Please explain.

The sum of the probabilities of all the outcomes of an experiment must be one.

An event that CANNOT happen has a negative probability.

Simulating an experiment with software gives theoretical probabilities.

What does it mean to say, "The probability of X is 0.8"?

Experiment: Toss four dishonest coins-penny, nickel, dime, quarter-with P(H) = 0.6 for each coin. A computer produced the table below for a simulation of the whole experiment 8000 times. ​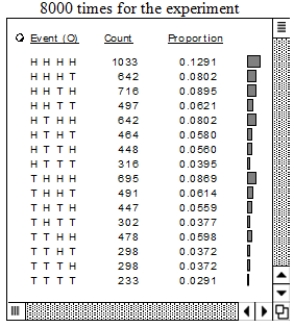 A) In the HHTT line (the fourth line in the body of the table), how did the computer calculate to get 0.0621? B) What is the probability of at least one head (H), according to this simulation? ​

You may wish to use randomly selected digits efficiently to simulate this experiment. Experiment: Draw a ball from a bag that has 11 black balls (B), 5 red balls (R), and 4 green balls (G), and note its color. A) Tell what your code would be if you use two-digit numbers. Use an efficient code, omitting as few numbers as you can. 00 01 02 03 …………………………………………………… 97 98 99 B) Use the following from our table of randomly selected digits to simulate the experiment above 15 times efficiently. 11517 87601 71480 49210 81314 84069 64343 65909 23870 10394 8854 96029 C) What is the theoretical probability of getting a green ball? D) What is the probability of getting a green ball from your simulation in part B? E) Explain the difference between the answer in part C and the answer in part D.

One basketball player hits 46% of her shots. A) Give a code for hits and a code for misses so that one could use the table of randomly selected digits to simulate shots by the player. B) If you use your code two times to simulate 300 shots each time, will you get the same results both times? Explain why/why not.

In an experiment with two outcomes, each outcome must have probability 50%.

Simulating an experiment with randomly generated numbers gives experimental probabilities.

Design a simulation for a spinner that would allow a simulation of a birth happening during any of the 12 months of the year with equal probabilities. Describe how you would carry out the simulation.