Exam 19: Ordinary Differential Equations
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Write the single differential equation 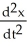 - 3
- 3 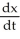 + 5x = 0 as an equivalent linear system using the change of variables x = u and
+ 5x = 0 as an equivalent linear system using the change of variables x = u and 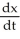 = v.
= v.
Free
(Essay)
4.8/5  (34)
(34)
Correct Answer:
(i) x = u ...... (1)
Differentiating both sides of (1) with respect to t we obtain
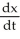 =
= 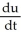 . Now
. Now 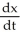 = v ;
= v ;
hence 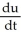 = v ........... (2)
= v ........... (2)
Next 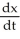 = v ...... (3)
= v ...... (3)
Find the eigenvalues of the linear system 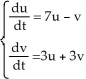 .
.
Free
(Multiple Choice)
4.8/5  (28)
(28)
Correct Answer:
D
Use the Runge-Kutta method with step size h = 0.1 to approximate the solution of the initial-value problem 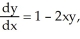
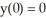 on the interval
on the interval 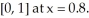
(Multiple Choice)
4.9/5  (25)
(25)
Use the improved Euler method to determine an approximate value of the solution of the initial-value problem 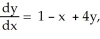
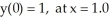 using step size
using step size 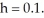
(Multiple Choice)
4.7/5  (35)
(35)
An LCR circuit consists of a resistor R (having resistance R measured in ohms), a capacitor C (having capacitance C measured in farads), and an inductor L (having inductance L measured in henries) and connected in a series together with an electromotive force (such as a battery or generator) E (measured in volts V).By Kirchhoff's law, the current i (measured in amperes) satisfies the differential equation L 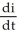 + Ri +
+ Ri + 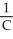
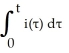 = E(t).
Let L = 10 henries, R = 0 ohms, C = 0.1 farad, and E(t) = 20 cos(t).
Determine the current i at any time t ≥ 0 if the current is zero at t = 0.
= E(t).
Let L = 10 henries, R = 0 ohms, C = 0.1 farad, and E(t) = 20 cos(t).
Determine the current i at any time t ≥ 0 if the current is zero at t = 0.
(Short Answer)
4.7/5  (29)
(29)
Solve the differential equation (3y + 8x 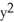 ) dx + (x + 4
) dx + (x + 4 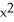 y) dy = 0 by finding an integrating factor depending on x.
y) dy = 0 by finding an integrating factor depending on x.
(Multiple Choice)
4.7/5  (36)
(36)
State the order of the following differential equation and whether it is linear or nonlinear: 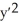 = xy.
= xy.
(Multiple Choice)
4.9/5  (37)
(37)
State the order of the following differential equation and whether it is linear or nonlinear: 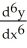 = 3x.
= 3x.
(Multiple Choice)
4.9/5  (39)
(39)
Let F(t) = 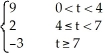 .Express F(t) in terms of the Heaviside function H(t -a
.Express F(t) in terms of the Heaviside function H(t -a
(Multiple Choice)
4.8/5  (38)
(38)
Find the general solution of the differential equation 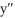 - 10
- 10 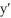 + 74y = 0.
+ 74y = 0.
(Multiple Choice)
4.8/5  (38)
(38)
The change of dependent variable y =  transforms the equation x
transforms the equation x 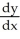 + y = x
+ y = x 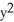 cos(x) into
cos(x) into
(Multiple Choice)
4.8/5  (35)
(35)
Solve the following initial-value problem: 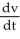 = 9.8 - 0.196v, v(0) = 48.
= 9.8 - 0.196v, v(0) = 48.
(Multiple Choice)
4.8/5  (31)
(31)
The fixed point at the origin of the autonomous linear system 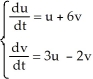 is
is
(Multiple Choice)
4.8/5  (35)
(35)
A body of mass m =  (kg) is attached to the end of a spring with Hooke's constant k = 50 (N/m) and is set in motion with initial position x(0) =
(kg) is attached to the end of a spring with Hooke's constant k = 50 (N/m) and is set in motion with initial position x(0) =  (m) and initial velocity
(m) and initial velocity 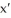 (0) = - 10 (m/s). (The mass is displaced to the right and moving to the left at time t = 0.)Find (a) the position x(t) of the body at later times t, (b) the amplitude, (c) frequency, and (d) period of its oscillation.
(0) = - 10 (m/s). (The mass is displaced to the right and moving to the left at time t = 0.)Find (a) the position x(t) of the body at later times t, (b) the amplitude, (c) frequency, and (d) period of its oscillation.
(Essay)
4.8/5  (29)
(29)
Find a homogeneous linear second-order differential equation with constant coefficient having general solution y = 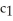
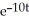 +
+ 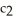 t
t 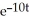 .
.
(Multiple Choice)
4.7/5  (34)
(34)
Find a particular solution of the differential equation 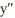 + y = 8sin x - 6 cos(x).
+ y = 8sin x - 6 cos(x).
(Multiple Choice)
4.9/5  (35)
(35)
Find the solution of the initial value problem 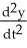 + 4y = F(t), y(0) = 0 ,
+ 4y = F(t), y(0) = 0 , 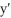 (0) = - 1, whereF(t) =
(0) = - 1, whereF(t) = 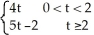 .
.
(Essay)
4.8/5  (33)
(33)
Showing 1 - 20 of 135
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)