Exam 8: Applications of Integration
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Let R be the plane region enclosed by the trapezoid with vertices at the points (0, 0), (1, 1), (5, 1), and (6, 0).(i) Find the y-coordinate of the centroid of the region R.(ii) Use Pappus's Theorem to find the volume of the solid generated by revolving the region R about the x-axis.
Free
(Essay)
4.9/5  (29)
(29)
Correct Answer:
(i)  =
= 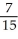 (ii) Volume V =
(ii) Volume V = 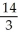 π cubic units
π cubic units
Solve the following initial-value problem: 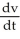 = 9.8 - 0.196v,v(0) = 48.
= 9.8 - 0.196v,v(0) = 48.
Free
(Multiple Choice)
4.9/5  (32)
(32)
Correct Answer:
B
The price of a computer chip t months after it is introduced to the market is given by $C where 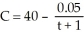 and the number sold per month at that time is N = 6,000 + 10t.To the nearest thousand dollars, how much income is derived from the sales of these chips over the first year?
and the number sold per month at that time is N = 6,000 + 10t.To the nearest thousand dollars, how much income is derived from the sales of these chips over the first year?
Free
(Multiple Choice)
4.8/5  (36)
(36)
Correct Answer:
C
Find the volume of the solid ring obtained by rotating the disc x2 + 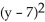 = 9 about the x-axis.
= 9 about the x-axis.
(Multiple Choice)
4.8/5  (38)
(38)
A cube has edge length a cm and one corner at position O. A plane passing through the three corners of the cube that are adjacent to corner O slices the cube into two pieces. Find the volume of the smaller piece.
(Multiple Choice)
4.9/5  (52)
(52)
Find the moment about the x-axis of a plate of constant areal density 1 occupying the finite plane region bounded by the x-axis and the curve y = -16 + 10x - 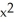 .
.
(Multiple Choice)
4.8/5  (34)
(34)
Find the area of the oval surface obtained by rotating the ellipse 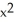 + 4
+ 4 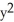 = 1 about its major axis (i.e., about the x-axis).
= 1 about its major axis (i.e., about the x-axis).
(Multiple Choice)
4.8/5  (38)
(38)
Find the volume of the solid generated by revolving the plane region bounded by the graphs of 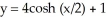 and the line y = 3 from x = 0 to x = 2ln(2) about the x-axis.
and the line y = 3 from x = 0 to x = 2ln(2) about the x-axis.
(Multiple Choice)
4.8/5  (37)
(37)
Find the mean μ and the standard deviation σ of a random variable X distributed uniformly on the interval [2 - 4 ![Find the mean μ and the standard deviation σ of a random variable X distributed uniformly on the interval [2 - 4 , 2 + 4 ].](https://storage.examlex.com/TB9661/11ee77e1_77f9_554a_a0f8_17cb3294b47f_TB9661_11.jpg) , 2 + 4
, 2 + 4 ![Find the mean μ and the standard deviation σ of a random variable X distributed uniformly on the interval [2 - 4 , 2 + 4 ].](https://storage.examlex.com/TB9661/11ee77e1_77f9_554b_a0f8_7d101d2774f0_TB9661_11.jpg) ].
].
(Short Answer)
4.9/5  (29)
(29)
Determine a multiplier (integrating factor) of the first order linear differential equation+ 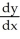
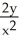 = x.
= x.
(Multiple Choice)
4.9/5  (38)
(38)
Find the solution of the initial-value problem 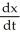 =
= 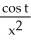 , x(0) = 5.
, x(0) = 5.
(Multiple Choice)
4.8/5  (42)
(42)
Find the area of the surface generated by rotating y = ![Find the area of the surface generated by rotating y = - where x [0, 3] about y = 0.](https://storage.examlex.com/TB9661/11ee77e1_77f4_e8b0_a0f8_d16a73ccaffa_TB9661_11.jpg) -
- ![Find the area of the surface generated by rotating y = - where x [0, 3] about y = 0.](https://storage.examlex.com/TB9661/11ee77e1_77f4_e8b1_a0f8_ddaef5c36335_TB9661_11.jpg) where x
where x ![Find the area of the surface generated by rotating y = - where x [0, 3] about y = 0.](https://storage.examlex.com/TB9661/11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11.jpg) [0, 3] about y = 0.
[0, 3] about y = 0.
(Multiple Choice)
4.8/5  (32)
(32)
A finite region R is contained in the first quadrant of the xy-plane. The centroid of R is the point (3, h). When R is revolved about the y-axis it generates a solid having volume 12 cubic units. When R is revolved about the x-axis it generates a solid having volume 32 cubic units. Find (a) the area of R and (b) the value of h.
(Multiple Choice)
4.8/5  (29)
(29)
A ball of radius r has volume V(r) = 
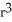 cubic units. This volume can be regarded as a sum of volumes of concentric spherical shells having radii x units (where 0 x r) and thickness dx. Use this fact to find the surface area S(r) of a sphere of radius r.
cubic units. This volume can be regarded as a sum of volumes of concentric spherical shells having radii x units (where 0 x r) and thickness dx. Use this fact to find the surface area S(r) of a sphere of radius r.
(Multiple Choice)
4.9/5  (40)
(40)
Find the area of the surface generated by rotating 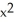 +
+ 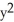 =
= 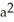 about y = a.
about y = a.
(Multiple Choice)
4.9/5  (34)
(34)
Showing 1 - 20 of 139
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)