Exam 15: Functions of Several Variables
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Compute the gradient of the function at the given point.
-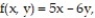
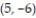
(Multiple Choice)
4.9/5  (29)
(29)
Determine whether the given function satisfies a Laplace equation.
-f(x, y) = 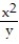
(True/False)
4.8/5  (33)
(33)
Find all the first order partial derivatives for the following function.
-f(x, y) = 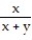
(Multiple Choice)
4.8/5  (29)
(29)
Find all local extreme values of the given function and identify each as a local maximum, local minimum, or saddle point.
-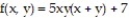
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-Evaluate 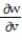 at (u, v) = ( 5, 4) for the function w(x, y) = x
at (u, v) = ( 5, 4) for the function w(x, y) = x 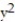 - ln x; x =
- ln x; x = 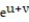 , y = uv.
, y = uv.
(Multiple Choice)
4.9/5  (40)
(40)
Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-f(x, y) = 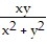
(Short Answer)
4.8/5  (42)
(42)
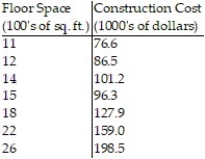
Solve the problem.
-The table below summarizes the construction cost of a set of homes (excluding the lot cost) along with the square footage of the home's floor space. Find a linear equation that relates the construction cost in thousands of dollars to the floor space in hundreds of square feet by finding the least squares line for the data.
(Multiple Choice)
4.8/5  (27)
(27)
Find the absolute maxima and minima of the function on the given domain.
- 
(Multiple Choice)
4.8/5  (26)
(26)
Use implicit differentiation to find the specified derivative at the given point.
-Find 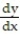 at the point (1, -1) for 3x
at the point (1, -1) for 3x 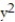 + 2
+ 2 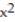 y - 3x = 0.
y - 3x = 0.
(Multiple Choice)
4.8/5  (36)
(36)
Determine whether the function is a solution of the wave equation.
-w(x, t) = 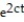 cos 2x
cos 2x
(True/False)
4.8/5  (25)
(25)
Solve the problem.
-The radius r and height h of a cylinder are changing with time. At the instant in question, 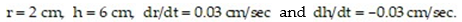 At what rate is the cylinder's volume changing at that instant?
At what rate is the cylinder's volume changing at that instant?
(Multiple Choice)
4.9/5  (30)
(30)
Solve the problem.
-Find the derivative of the function 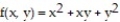 at the point
at the point 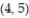 in the direction in which the function increases most rapidly.
in the direction in which the function increases most rapidly.
(Multiple Choice)
4.8/5  (37)
(37)
Find the extreme values of the function subject to the given constraint.
-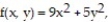
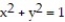
(Multiple Choice)
4.9/5  (34)
(34)
Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-f(x, y) = 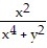
(Short Answer)
4.8/5  (27)
(27)
Use implicit differentiation to find the specified derivative at the given point.
-Find 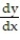 at the point (-1, 1) for 2x -
at the point (-1, 1) for 2x -  + 2
+ 2 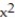
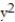 = 0.
= 0.
(Multiple Choice)
4.8/5  (41)
(41)
Find the derivative of the function at the given point in the direction of A.
-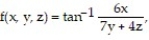
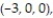
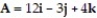
(Multiple Choice)
4.8/5  (30)
(30)
Solve the problem.
-Write an equation for the tangent line to the curve 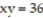 at the point
at the point 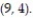
(Multiple Choice)
4.8/5  (35)
(35)
Find the absolute maxima and minima of the function on the given domain.
-f(x, y) = 9x + 4y on the trapezoidal region with vertices (0, 0), (1, 0), (0, 2), and (1, 1)
(Multiple Choice)
4.9/5  (24)
(24)
Use polar coordinates to find the limit of the function as (x, y) approaches (0, 0).
-f(x, y) = cos 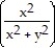
(Multiple Choice)
4.8/5  (35)
(35)
Showing 201 - 220 of 229
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)