Exam 15: Functions of Several Variables
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
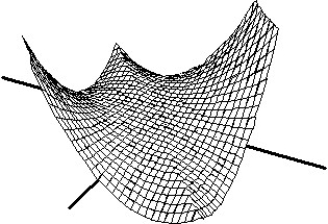
Match the surface show below to the graph of its level curves.
-
(Multiple Choice)
4.9/5  (35)
(35)
Use polar coordinates to find the limit of the function as (x, y) approaches (0, 0).
-f(x, y) = 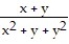
(Multiple Choice)
4.9/5  (28)
(28)
Use implicit differentiation to find the specified derivative at the given point.
-Find 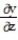 at the point ( 1, 3, 2) for
at the point ( 1, 3, 2) for 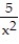 +
+ 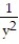 +
+ 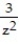 = 0.
= 0.
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-Evaluate 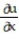 at (x, y, z) = ( 1, 2, 1) for the function u(p, q, r) =
at (x, y, z) = ( 1, 2, 1) for the function u(p, q, r) = 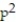 -
- 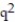 - r; p = xy, q =
- r; p = xy, q = 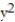 , r = xz.
, r = xz.
(Multiple Choice)
4.8/5  (28)
(28)
Solve the problem.
-Find the least squares line through the points 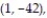
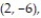 and
and 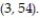
(Multiple Choice)
4.8/5  (36)
(36)
Provide an appropriate response.
-Find the direction in which the function is increasing most rapidly at the point 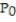 . f(x, y, z) = xy - ln(z),
. f(x, y, z) = xy - ln(z), 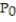 ( 1, 2, 2)
( 1, 2, 2)
(Multiple Choice)
4.7/5  (33)
(33)
Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-f(x, y) = 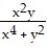
(Short Answer)
4.8/5  (47)
(47)
Find all the first order partial derivatives for the following function.
-f(x, y) = 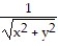
(Multiple Choice)
4.9/5  (22)
(22)
Use implicit differentiation to find the specified derivative at the given point.
-Find 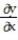 at the point (1, 2,
at the point (1, 2, 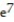 ) for ln
) for ln 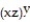 + 3
+ 3 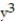 = 0.
= 0.
(Multiple Choice)
4.7/5  (33)
(33)
Find the extreme values of the function subject to the given constraint.
-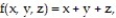
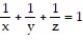
(Multiple Choice)
4.9/5  (40)
(40)
Find the linear approximation of the function at the given point.
-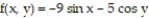 at
at 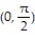
(Multiple Choice)
4.8/5  (38)
(38)
Write a chain rule formula for the following derivative.
-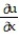 for u = f(p, q); p = g(x, y, z), q = h(x, y, z)
for u = f(p, q); p = g(x, y, z), q = h(x, y, z)
(Multiple Choice)
4.9/5  (50)
(50)
Find the derivative of the function at the given point in the direction of A.
-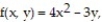
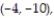 A = 3i- 4j
A = 3i- 4j
(Multiple Choice)
4.8/5  (40)
(40)
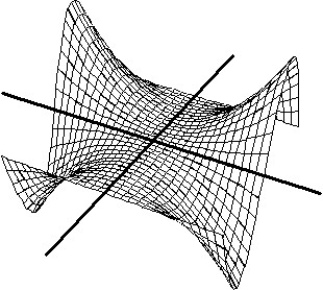
Match the surface show below to the graph of its level curves.
-
(Multiple Choice)
4.8/5  (28)
(28)
Find the extreme values of the function subject to the given constraint.
-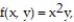
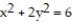
(Multiple Choice)
4.8/5  (35)
(35)
Find all local extreme values of the given function and identify each as a local maximum, local minimum, or saddle point.
-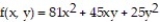
(Multiple Choice)
4.8/5  (27)
(27)
Showing 141 - 160 of 229
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)