Exam 15: Functions of Several Variables
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Find all the second order partial derivatives of the given function.
-f(x, y) = 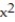 + y -
+ y - 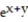
(Multiple Choice)
4.8/5  (31)
(31)
Find all the first order partial derivatives for the following function.
-f(x, y) = 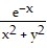
(Multiple Choice)
4.7/5  (35)
(35)
Solve the problem.
-Find the derivative of the function 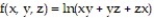 at the point
at the point 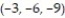 in the direction in which the function increases most rapidly.
in the direction in which the function increases most rapidly.
(Multiple Choice)
4.9/5  (37)
(37)
Find the extreme values of the function subject to the given constraint.
-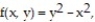
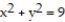
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-Find the derivative of the function 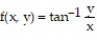 at the point
at the point 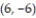 in the direction in which the function increases most rapidly.
in the direction in which the function increases most rapidly.
(Multiple Choice)
4.8/5  (31)
(31)
At what points is the given function continuous?
-f(x, y) = 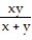
(Multiple Choice)
4.8/5  (34)
(34)
Find all the first order partial derivatives for the following function.
-f(x, y, z) = xz 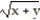
(Multiple Choice)
4.8/5  (38)
(38)
Find all the first order partial derivatives for the following function.
-f(x, y, z) = 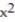 y +
y + 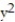 z + x
z + x 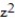
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-Find the point on the line 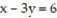 that is closest to the origin.
that is closest to the origin.
(Multiple Choice)
4.7/5  (33)
(33)
Write a chain rule formula for the following derivative.
-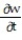 for w = f(p, q, r); p = g(t), q = h(t), r = k(t)
for w = f(p, q, r); p = g(t), q = h(t), r = k(t)
(Multiple Choice)
4.8/5  (28)
(28)
Find all the second order partial derivatives of the given function.
-f(x, y) = ln ( 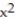 y - x)
y - x)
(Multiple Choice)
4.9/5  (34)
(34)
Find the absolute maxima and minima of the function on the given domain.
-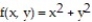 on the diamond-shaped region
on the diamond-shaped region 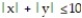
(Multiple Choice)
4.9/5  (27)
(27)
Solve the problem.
-According to the Gas Kinetic Theory, the average speed of a gas particle is given by 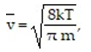 where
where
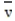 is the speed in m/s, k is the constant 1.38 × 10-23 , T is the temperature of the gas in Kelvin, and m is the mass of the gas particle in kg. What is the average speed of an oxygen molecule with a mass of
5.314 X 10-26 KG at a temperature of 500 K?
is the speed in m/s, k is the constant 1.38 × 10-23 , T is the temperature of the gas in Kelvin, and m is the mass of the gas particle in kg. What is the average speed of an oxygen molecule with a mass of
5.314 X 10-26 KG at a temperature of 500 K?
(Multiple Choice)
4.8/5  (36)
(36)
Write a chain rule formula for the following derivative.
-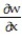 for w = f(p, q); p = g(x, y), q = h(x, y)
for w = f(p, q); p = g(x, y), q = h(x, y)
(Multiple Choice)
4.8/5  (41)
(41)
Find all local extreme values of the given function and identify each as a local maximum, local minimum, or saddle point.
-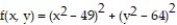
(Multiple Choice)
4.8/5  (36)
(36)
Find the domain and range and describe the level curves for the function f(x,y).
-f(x, y) = 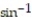 (
( 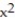 +
+ 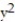 )
)
(Multiple Choice)
4.9/5  (33)
(33)
Find the extreme values of the function subject to the given constraint.
-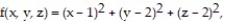
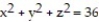
(Multiple Choice)
4.8/5  (42)
(42)
Showing 181 - 200 of 229
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)