Exam 15: Functions of Several Variables
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-f(x, y) = 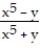
(Short Answer)
4.8/5  (37)
(37)
Use implicit differentiation to find the specified derivative at the given point.
-Find 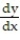 at the point (1, 1) for 7
at the point (1, 1) for 7 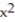 + 7
+ 7 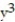 + 5xy = 0.
+ 5xy = 0.
(Multiple Choice)
4.8/5  (29)
(29)
Solve the problem.
-Find the equation for the tangent plane to the surface 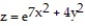 at the point
at the point 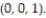
(Multiple Choice)
4.9/5  (32)
(32)
Find all local extreme values of the given function and identify each as a local maximum, local minimum, or saddle point.
-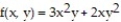
(Multiple Choice)
4.9/5  (36)
(36)
Determine whether the given function satisfies a Laplace equation.
-f(x, y) = 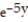 sin -5x
sin -5x
(True/False)
4.8/5  (34)
(34)
Solve the problem.
-Amarillo Motors manufactures an economy car called the Citrus, which is notorious for its inability to hold a respectable resale value. The average resale value of a set of 1998 Amarillo Citrus's is summarized in the table below along with the age of the car at the time of resale and the number of cars included in the average. Fit a line of the form ln(V) = m.a + b to the data, where V is the resale value in thousands of dollars and a is the age of the car in years.
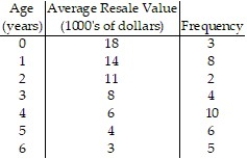
(Multiple Choice)
4.9/5  (40)
(40)
Find the derivative of the function at the given point in the direction of A.
-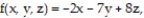
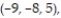
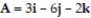
(Multiple Choice)
4.7/5  (46)
(46)
Determine whether the given function satisfies a Laplace equation.
-f(x, y, z) = 5x + 9 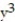
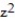
(True/False)
4.8/5  (29)
(29)
Provide an appropriate response.
-Find the direction in which the function is increasing most rapidly at the point 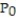 . f(x, y) = x
. f(x, y) = x 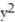 - y
- y 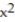 ,
, 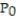 ( -1, 2)
( -1, 2)
(Multiple Choice)
4.9/5  (34)
(34)
Use polar coordinates to find the limit of the function as (x, y) approaches (0, 0).
-f(x, y) = 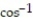
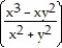
(Multiple Choice)
4.7/5  (38)
(38)
Find the linear approximation of the function at the given point.
-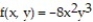 at
at 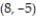
(Multiple Choice)
4.9/5  (36)
(36)
At what points is the given function continuous?
-f(x, y) = 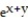
(Multiple Choice)
4.8/5  (42)
(42)
Determine whether the function is a solution of the wave equation.
-w(x, t) = 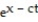
(True/False)
5.0/5  (36)
(36)
Find all local extreme values of the given function and identify each as a local maximum, local minimum, or saddle point.
-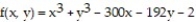
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-Find the points on the curve 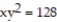 that are closest to the origin.
that are closest to the origin.
(Multiple Choice)
5.0/5  (41)
(41)
Showing 61 - 80 of 229
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)