Exam 6: Systems of Linear Equations and Matrices
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
The diagram shows the roads connecting four cities.
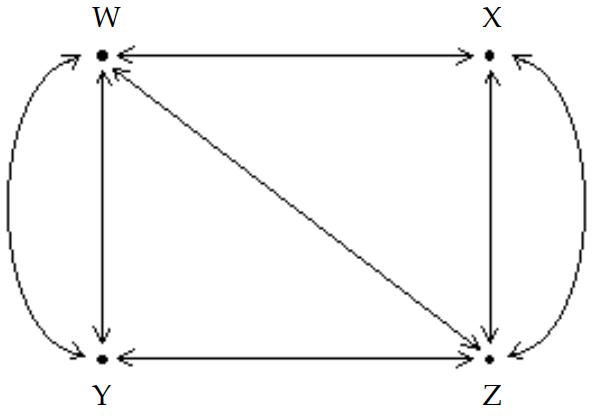 The matrix A below represents the number of routes between each pair of cities without passing through another city.
The matrix A below represents the number of routes between each pair of cities without passing through another city.
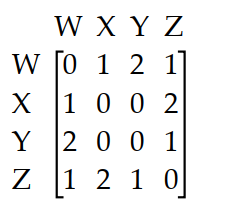 Calculate . What information is given by the entry in row 3, column 2 of ?
Calculate . What information is given by the entry in row 3, column 2 of ?
(Multiple Choice)
4.8/5  (37)
(37)
Use the Gauss-Jordan method to solve the system of equations.
-
(Multiple Choice)
4.9/5  (33)
(33)
a system of linear equations containing more equations than variables is always inconsistent.
(True/False)
4.8/5  (32)
(32)
Determine whether the two matrices are inverses of each other by computing their product.
-
(True/False)
4.8/5  (38)
(38)
Write a matrix to display the information.
-The matrix shows the average number of wax and buff treatments each of 3 workers in a car wash can do in a day. Give the matrix that shows what each worker can do in 3 days.
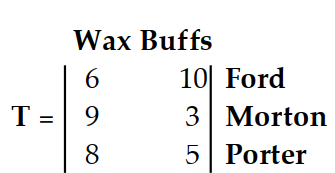
(Multiple Choice)
4.9/5  (25)
(25)
Write the word or phrase that best completes each statement or answers thequestion.
-Suppose the following matrix represents the input-output matrix of a simplified economy. How many units of each commodity should be produced to satisfy a demand of 1400 units for each commodity?
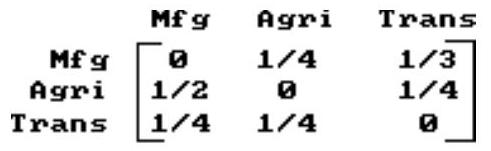
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-During rush hours, substantial traffic congestion is encountered at the intersections shown in the figure. The arrows indicate one-way streets. As the figure shows, 500 cars per hour come down P Street to intersection A, and 200 cars per hour come down 5th Street to intersection A. x of these cars leave A on P Street and w cars leave A on 5th Street.
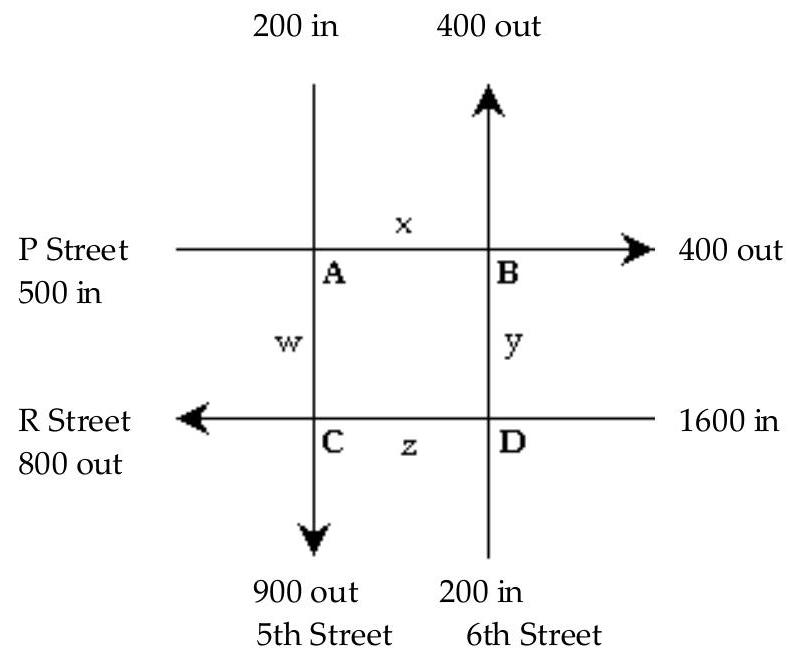 The number of cars entering intersection A must equal the number leaving, so that or . By writing an equation representing the traffic entering and leaving each of the intersections A, B, C, and D, obtain a system of four equations. Solve the system using as the parameter.
The number of cars entering intersection A must equal the number leaving, so that or . By writing an equation representing the traffic entering and leaving each of the intersections A, B, C, and D, obtain a system of four equations. Solve the system using as the parameter.
(Multiple Choice)
4.8/5  (36)
(36)
Find the production matrix for the input-output and demand matrices.
-
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-Three different clothing stores order the following amounts of clothing by a certain designer:
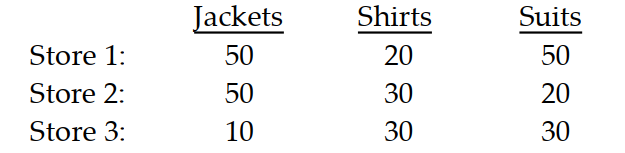 The unit prices of each product are given below for two suppliers:
The unit prices of each product are given below for two suppliers:
 What matrix product displays the cost to each store of buying the clothes from each supplier? Display the two matrices which must be multiplied and their product.
What matrix product displays the cost to each store of buying the clothes from each supplier? Display the two matrices which must be multiplied and their product.
(Multiple Choice)
4.8/5  (31)
(31)
The diagram shows the roads connecting four cities.
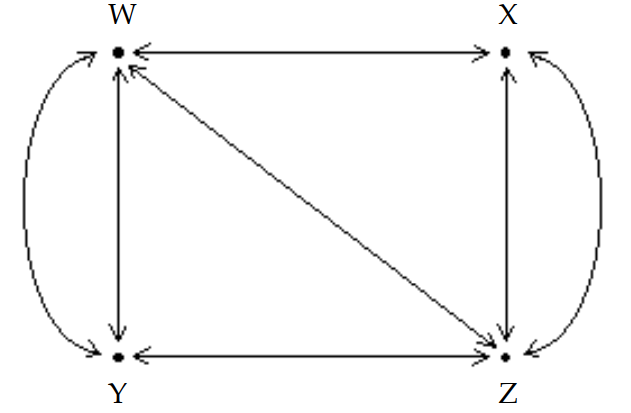 How many ways are there to travel between cities and by passing through exactly one city? (Hint: Write a matrix, A, to represent the number of routes between each pair of cities without passing through another city. Then calculate ).
How many ways are there to travel between cities and by passing through exactly one city? (Hint: Write a matrix, A, to represent the number of routes between each pair of cities without passing through another city. Then calculate ).
(Multiple Choice)
4.8/5  (27)
(27)
Solve the problem by writing and solving a suitable system of equations.
-Factories A and B sent rice to stores 1 and 2. A sent 12 loads and B sent 24 . Store 1 used 19 loads and store 2 used 17. It cost to ship from A to 1, \$350 from A to 2, from B to 1, and from B to 2 . was spent. How many loads went where?
(Multiple Choice)
4.8/5  (33)
(33)
Solve the problem by writing and solving a suitable system of equations.
-A company makes 3 types of cable. Cable A requires 3 black, 3 white, and 2 red wires. Cable B requires 1 black, 2 white, and 1 red wires. Cable requires 2 black, 1 white, and 2 red wires. They used 100 black, 110 white and 80 red wires. How many of each cable were made?
(Multiple Choice)
4.9/5  (27)
(27)
Write a matrix to display the information.
-Carney and Dobler sell home and mortgage insurance. Their sales for the months of May and June are given in the matrices.
 Find the matrix that would give the change in sales from May to June.
Find the matrix that would give the change in sales from May to June.
(Multiple Choice)
4.7/5  (38)
(38)
Showing 141 - 160 of 215
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)