Exam 6: Systems of Linear Equations and Matrices
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Determine whether the two matrices are inverses of each other by computing their product.
-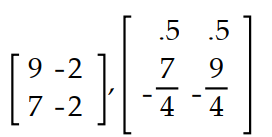
(True/False)
4.9/5  (29)
(29)
Determine whether the two matrices are inverses of each other by computing their product.
- and
(True/False)
4.7/5  (24)
(24)
Write the word or phrase that best completes each statement or answers the question
-Using the matrices and , verify that (matrix subtraction is not commutative).
(Essay)
4.9/5  (27)
(27)
Write a system of equations and use the inverse of the coefficient matrix to solve the system.
-A basketball fieldhouse seats 15,000 . Courtside seats sell for , endzone for , and balcony for . Total for a sell-out is . If half the courtside and balcony and all endzone seats are sold, the total is . How many of each type are there?
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem by writing and solving a suitable system of equations.
-Mike, Joe, and Bill are painting a fence. The painting can be finished if Mike and Joe work together for 4 hours and Bill works alone for 2 hours or if Mike and Joe work together for 2 hours and Bill works alone for 5 hours, or if Mike works alone for 6 hours, Joe works alone for 2 hours, and Bill works alone for 1 hour. How much time does it take for each man working alone to complete the painting?
(Multiple Choice)
4.7/5  (32)
(32)
Perform row operations on the augmented matrix as far as necessary to determine whether the system is independent,dependent, or inconsistent.
-
(Multiple Choice)
4.8/5  (39)
(39)
Solve the system by using the inverse of the coefficient matrix.
-
(Multiple Choice)
4.7/5  (40)
(40)
Write a matrix to display the information.
-A bakery sells three types of cakes. Cake I requires 2 cups of flour, 2 cups of sugar, and 2 eggs. Cake II requires 4 cups of flour, 1 cup of sugar, and 1 egg. Cake III requires 2 cups of flour, 2 cups of sugar, and 3 eggs. Make a matrix showing the required ingredients for each cake. Assign the cakes to the rows and the ingredients to the columns.
(Multiple Choice)
4.9/5  (38)
(38)
Obtain an equivalent system by performing the stated elementary operation on the system.
-Replace the fourth equation by the sum of itself and 3 times the second equation
X-2 y+5 z-6 w=4 \\
4 y-z+4 w=-5 \\
3 y-4 z+2 w=-3 \\
2 y-2 z-3 w=8
(Multiple Choice)
4.8/5  (40)
(40)
Find the production matrix for the input-output and demand matrices.
-
(Multiple Choice)
4.8/5  (47)
(47)
Solve the system of equations. If the system is dependent, express solutions in terms of the parameter .
-
(Multiple Choice)
4.9/5  (34)
(34)
Given the matrices and , find the matrix product .
- Find .
(Multiple Choice)
4.9/5  (28)
(28)
Determine whether the given ordered set of numbers is a solution of the system of equations.
-
(True/False)
4.9/5  (18)
(18)
Multiply both sides of each equation by a common denominator to eliminate the fractions. Then solve the system.
-
(Multiple Choice)
4.8/5  (34)
(34)
a system of linear equations containing more variables than equations is always dependent.
(True/False)
4.7/5  (43)
(43)
Solve the problem.
-Suppose the following matrix represents the input-output matrix of a primitive economy. How much of each commodity should be produced to produce 89 bushels of yams and 60 pigs?

(Multiple Choice)
4.8/5  (38)
(38)
The diagram shows the roads connecting four cities. Write a matrix to represent the number of routes between each pair of cities without passing through another city.
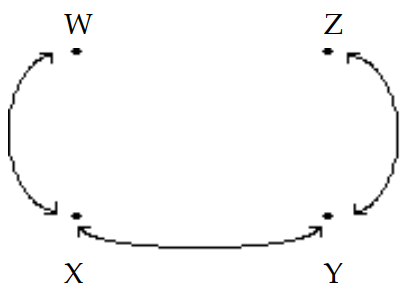
(Multiple Choice)
4.9/5  (29)
(29)
The diagram shows the roads connecting four cities.
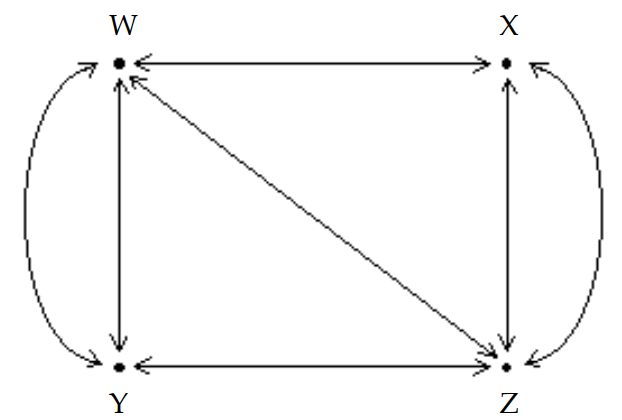 How many ways are there to travel between cities and by passing through exactly two cities? (Hint: Write a matrix, A, to represent the number of routes between each pair of cities without passing through another city. Then calculate and ).
How many ways are there to travel between cities and by passing through exactly two cities? (Hint: Write a matrix, A, to represent the number of routes between each pair of cities without passing through another city. Then calculate and ).
(Multiple Choice)
4.8/5  (42)
(42)
Showing 41 - 60 of 215
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)