Exam 6: Systems of Linear Equations and Matrices
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Use the Gauss-Jordan method to solve the system of equations.
-
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem by writing and solving a suitable system of equations.
-A small business takes out loans from three different banks to buy some new equipment. The total amount of the three loans is . The first bank offered an interest rate of . The second bank offered a rate of and the amount borrowed from this bank was less than twice as much as the amount borrowed from the first bank. The third bank offered a rate of . The total annual interest was . How much did they borrow from each bank?
(Multiple Choice)
4.7/5  (33)
(33)
Find the order of the matrix product and the product , whenever the products exist.
- is is .
(Multiple Choice)
4.8/5  (31)
(31)
The diagram shows the roads connecting four cities.
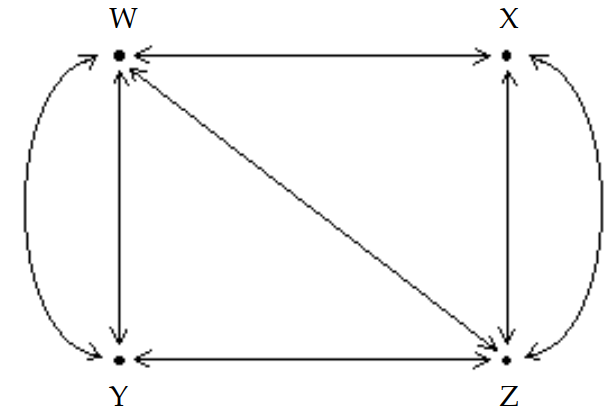 How many ways are there to travel between cities and by passing through exactly two cities? (Hint: Write a matrix, A, to represent the number of routes between each pair of cities without passing through another city. Then calculate and ).
How many ways are there to travel between cities and by passing through exactly two cities? (Hint: Write a matrix, A, to represent the number of routes between each pair of cities without passing through another city. Then calculate and ).
(Multiple Choice)
4.7/5  (33)
(33)
Determine whether the given ordered set of numbers is a solution of the system of equations.
-
(True/False)
4.8/5  (36)
(36)
Determine whether the two matrices are inverses of each other by computing their product.
-
(True/False)
4.9/5  (34)
(34)
Given the matrices and , find the matrix product .
- Find .
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem by writing and solving a suitable system of equations.
-Carole's car averages 13.0 miles per gallon in city driving and 21.0 miles per gallon in highway driving. If she drove a total of 443.0 miles on 23 gallons of gas, how many of the gallons were used for city driving?
(Multiple Choice)
4.9/5  (38)
(38)
Given the matrices and , find the matrix product .
- Find .
(Multiple Choice)
4.8/5  (31)
(31)
Find the order of the matrix product and the product , whenever the products exist.
- is is .
(Multiple Choice)
4.8/5  (31)
(31)
Multiply both sides of each equation by a common denominator to eliminate the fractions. Then solve the system.
-
(Multiple Choice)
4.8/5  (35)
(35)
Determine whether the two matrices are inverses of each other by computing their product.
-
(True/False)
4.9/5  (31)
(31)
Solve the system by using the inverse of the coefficient matrix.
-
(Multiple Choice)
4.8/5  (41)
(41)
Obtain an equivalent system by performing the stated elementary operation on the system.
-Replace the third equation by the sum of itself and -1 times the second equation.
(Multiple Choice)
4.9/5  (37)
(37)
Obtain an equivalent system by performing the stated elementary operation on the system.
-Interchange equations 1 and 3.
(Multiple Choice)
4.8/5  (45)
(45)
Perform row operations on the augmented matrix as far as necessary to determine whether the system is independent,dependent, or inconsistent.
-
(Multiple Choice)
4.8/5  (46)
(46)
The diagram shows the roads connecting four cities.
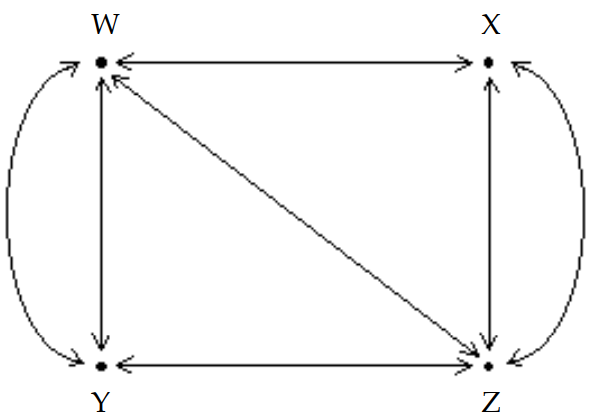 How many ways are there to travel between cities and by passing through at most one city? (Hint: Write a matrix, A, to represent the number of routes between each pair of cities without passing through another city. Then calculate ).
How many ways are there to travel between cities and by passing through at most one city? (Hint: Write a matrix, A, to represent the number of routes between each pair of cities without passing through another city. Then calculate ).
(Multiple Choice)
4.9/5  (36)
(36)
Showing 81 - 100 of 215
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)