Exam 6: Systems of Linear Equations and Matrices
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Solve the system by using the inverse of the coefficient matrix.
-
(Multiple Choice)
4.8/5  (40)
(40)
Given the matrices and , find the matrix product .
- Find .
(Multiple Choice)
4.8/5  (25)
(25)
The diagram shows the roads connecting four cities. Write a matrix to represent the number of routes between each pair of cities without passing through another city.
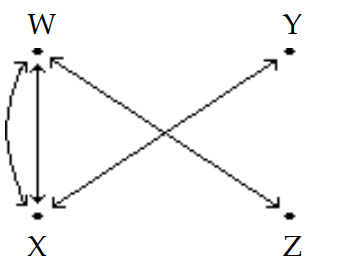
(Multiple Choice)
5.0/5  (41)
(41)
Solve the problem by writing and solving a suitable system of equations.
-Alan invests a total of in three different ways. He invests one part in a mutual fund which in the first year has a return of . He invests the second part in a government bond at per year. The third part he puts in the bank at per year. He invests twice as much in the mutual fund as in the bank. The first year Alan's investments bring a total return of . How much did he invest in each way?
(Multiple Choice)
4.8/5  (35)
(35)
Write a system of equations and use the inverse of the coefficient matrix to solve the system.
-A company makes 3 types of cable. Cable A requires 3 black, 3 white, and 2 red wires. Cable B requires 1 black, 2 white, and 1 red wires. Cable requires 2 black, 1 white, and 2 red wires. They used 100 black, 110 white and 80 red wires. How many of each cable were made?
(Multiple Choice)
4.9/5  (30)
(30)
Given the matrices and , find the matrix product .
- Find .
(Multiple Choice)
4.8/5  (36)
(36)
Solve the system by using the inverse of the coefficient matrix.
-
(Multiple Choice)
4.8/5  (47)
(47)
Use the Gauss-Jordan method to solve the system of equations.
-
(Multiple Choice)
4.8/5  (27)
(27)
Solve the problem.
-The profits (in millions of dollars) of a company can be described by the equation , where is the number of years since 2000 . Profits were million in the year 2000, million in 2004, and million in 2008 . Find the values of , and and use your answer to estimate profits in the year 2014. Round to the nearest tenth.
(Multiple Choice)
4.7/5  (34)
(34)
Perform row operations on the augmented matrix as far as necessary to determine whether the system is independent,dependent, or inconsistent.
-
(Multiple Choice)
4.9/5  (27)
(27)
Write the word or phrase that best completes each statement or answers thequestion.
-A simplified economy is based on agriculture, manufacturing, and transportation. Each unit of agricultural output requires 0.3 unit of its own output, 0.5 of manufacturing, and 0.2 unit of transportation output. Each unit of manufacturing output requires 0.3 unit of its own output, 0.1 of agricultural, and 0.4 unit of transportation output. Each unit of transportation output requires 0.4 unit of its own output, 0.2 of agricultural, and 0.1 of manufacturing output. There is demand for 40 units of agricultural, 60 units of manufacturing, and 30 units of transportation output. How many units should each segment of the economy produce?
(Short Answer)
4.8/5  (37)
(37)
If is a matrix and is the zero matrix, what can you say about the matrix?
(Multiple Choice)
4.8/5  (36)
(36)
Solve the system by using the inverse of the coefficient matrix.
-
(Multiple Choice)
4.8/5  (35)
(35)
Perform row operations on the augmented matrix as far as necessary to determine whether the system is independent,dependent, or inconsistent.
-
(Multiple Choice)
4.9/5  (37)
(37)
Perform the row operations on the matrix and write the resulting matrix.
-Replace by
(Multiple Choice)
4.8/5  (36)
(36)
Multiply both sides of each equation by a common denominator to eliminate the fractions. Then solve the system.
-
(Multiple Choice)
4.9/5  (37)
(37)
Showing 61 - 80 of 215
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)