Exam 6: Systems of Linear Equations and Matrices
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Solve the problem by writing and solving a suitable system of equations.
-Best Rentals charges a daily fee plus a mileage fee for renting its cars. Barney was charged for 3 days and 300 miles, while Mary was charged for 5 days and 600 miles. What does Best Rental charge per day and per mile?
(Multiple Choice)
4.8/5  (39)
(39)
Given the matrices and , find the matrix product .
- Find .
(Multiple Choice)
4.9/5  (26)
(26)
Write a matrix to display the information.
-The matrices give points and rebounds for five starting players in two games. Find the matrix that gives the totals.
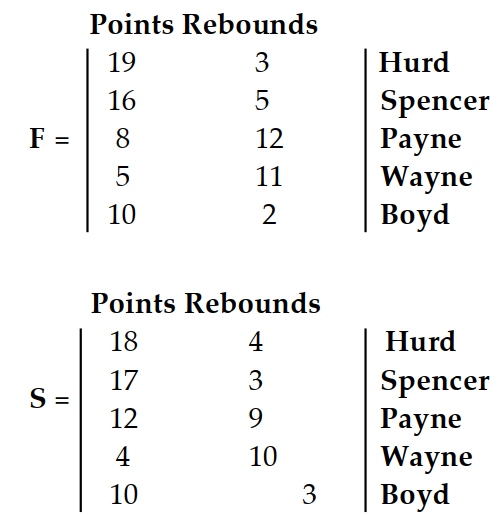
(Multiple Choice)
4.9/5  (31)
(31)
Solve the system by using the inverse of the coefficient matrix.
-
(Multiple Choice)
4.8/5  (31)
(31)
Solve the system by using the inverse of the coefficient matrix.
-
(Multiple Choice)
4.8/5  (30)
(30)
Solve the system of equations. If the system is dependent, express solutions in terms of the parameter .
-
(Multiple Choice)
5.0/5  (44)
(44)
Determine whether the given ordered set of numbers is a solution of the system of equations.
-(-6,-2)
(True/False)
4.8/5  (31)
(31)
Solve the problem by writing and solving a suitable system of equations.
-If 40 pounds of tomatoes and 20 pounds of bananas cost and 10 pounds of tomatoes and 30 pounds of bananas cost , what is the price per pound of tomatoes and bananas
(Multiple Choice)
4.7/5  (32)
(32)
Given the matrices and , find the matrix product .
- Find .
(Multiple Choice)
4.8/5  (32)
(32)
Find the production matrix for the input-output and demand matrices.
-
(Multiple Choice)
4.9/5  (32)
(32)
given a system of two linear equations in two variables, if the graphs of the two equations coincide, then the system is independent.
(True/False)
4.9/5  (36)
(36)
Use the Gauss-Jordan method to solve the system of equations.
-
(Multiple Choice)
5.0/5  (38)
(38)
Perform row operations on the augmented matrix as far as necessary to determine whether the system is independent,dependent, or inconsistent.
-
(Multiple Choice)
4.8/5  (37)
(37)
Write the word or phrase that best completes each statement or answers the question
-Using the matrices , and , verify that .
(Essay)
4.9/5  (27)
(27)
given a system of two linear equations in two variables, if the graphs of the two equations are distinct parallel lines, then the system has no solution.
(True/False)
4.9/5  (31)
(31)
Showing 181 - 200 of 215
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)