Exam 9: Counting, Probability Distributions, and Further Topics in Probability
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Use the multiplication principle to solve the problem.
-If 11 newborn babies are randomly selected, how many different gender sequences are possible?
(Multiple Choice)
4.9/5  (39)
(39)
A die is rolled 20 times and the number of twos that come up is tallied. Find the probability of getting the given result.
-More than three twos
(Multiple Choice)
4.9/5  (27)
(27)
Solve the problem.
-A contractor is considering a sale that promises a profit of with a probability of .7 or a loss (due to bad weather, strikes, and such) of with a probability of .3 . What is the expected profit?
(Multiple Choice)
5.0/5  (43)
(43)
Find the requested long-range probabilities based on the transition matrix or data given.
-The probability that an assembly line works correctly depends on whether the line worked correctly the last time. Find the long range probability that the line will work correctly.

(Multiple Choice)
5.0/5  (45)
(45)
Find the probability of the event.
-A 10-question multiple choice test has 4 possible answers for each question. A student selects at least 6 correct answers.
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-Awards are to be presented to seven people: Jeff, Karen, Lyle, Maria, Norm, Olivia, and Paul. How many different orders are possible for the awards if Maria and Olivia must be next to each other?
(Multiple Choice)
4.8/5  (29)
(29)
Solve the problem.
-At age 50, Ann must choose between taking at age 60 if she is alive then, or at age 70 if she is alive then. The probability for a person aged 50 living to be 60 and 70 is .88 and . 63 , respectively. Using expected value, what is Ann's best option?
(Multiple Choice)
4.8/5  (36)
(36)
Prepare a probability distribution for the experiment. Let represent the random variable, and let represent theprobability.
-Three cards are drawn from a deck. The number of kings is counted.
(Multiple Choice)
4.8/5  (33)
(33)
Solve the problem.
-A male decreases his life expectancy by 1 year on average, for every point that his blood pressure is above 120. The average life expectancy is 76 years. Find the life expectancy for a male whose blood pressure is 124 .
(Multiple Choice)
4.9/5  (31)
(31)
Use the payoff matrix to determine the best strategy.
-A clothing manufacturer must decide which of two clothing lines to emphasize for the spring season, her usual line or a budget line. Her success with each line depends on the state of the economy next year. She estimates the payoff matrix to be as follows:
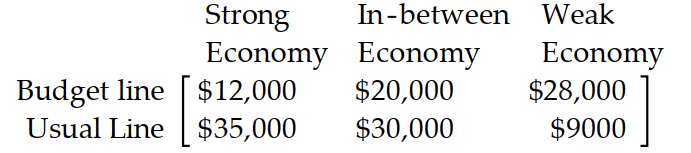 What is the manufacturer's best strategy if she is an optimist?
What is the manufacturer's best strategy if she is an optimist?
(Multiple Choice)
4.8/5  (32)
(32)
Find the expected value of the random variable in the experiment.
-Three cards are drawn from a deck without replacement. The number of aces is counted.
(Multiple Choice)
4.8/5  (35)
(35)
In a certain college, of the physics majors belong to ethnic minorities. Find the probability of the event from arandom sample of 10 students who are physics majors.
-Exactly 2 belong to an ethnic minority.
(Multiple Choice)
4.9/5  (30)
(30)
Find the requested probability.
-A child rolls a 6-sided die 6 times. What is the probability of the child rolling no more than three twos?
(Multiple Choice)
4.9/5  (31)
(31)
Find the requested long-range probabilities based on the transition matrix or data given.
-Weather is classified as fair, cloudy or rainy in a certain place. The probability that it will be fair, cloudy, or rainy on a given day depends on the weather the previous day. The transition matrix is given below. Find the long-range prediction for the proportion of fair, cloudy, and rainy days.
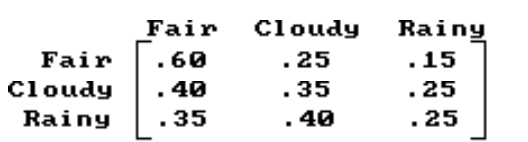
(Multiple Choice)
4.7/5  (35)
(35)
Construct the transition diagram and the transition matrix that represents the data.
-If it snows today, there is a(n) 70 percent chance of snow tomorrow; however if it does not snow today, there is a(n) 80 percent chance that it will not snow tomorrow.
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-At the first tri-city meeting, there were 8 people from town people from town , and 5 people from town C. If the council consists of 5 people, find the probability of 2 from town from town , and 1 from town .
(Multiple Choice)
4.9/5  (30)
(30)
Solve the problem.
-Estimate the probability that at least 2 of the 50 state governors have the same birthday.
(Multiple Choice)
4.7/5  (25)
(25)
Showing 141 - 160 of 210
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)