Exam 9: Counting, Probability Distributions, and Further Topics in Probability
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Use the payoff matrix to determine the best strategy.
-A college is holding a rock and roll concert to be held in the stadium and has sold out all tickets. If it rains, the show will have to be moved to the gym which has a smaller seating capacity. The college must decide in advance whether to set up seats and the stage in the gym, or in the stadium, or both, just in case. The net profit in each case is given in the payoff matrix below:
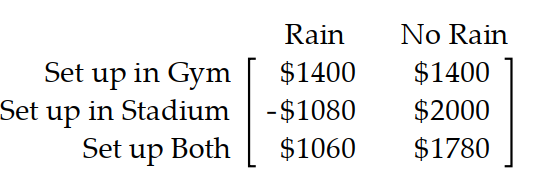 According to the weather forecaster, the probability of rain is 0.1 . What strategy should the organizer choose to maximize expected profit?
According to the weather forecaster, the probability of rain is 0.1 . What strategy should the organizer choose to maximize expected profit?
(Multiple Choice)
4.7/5  (38)
(38)
A die is rolled five times and the number of fours that come up is tallied. Find the probability of getting the given result.
-Exactly five fours
(Multiple Choice)
4.7/5  (36)
(36)
Prepare a probability distribution for the experiment. Let represent the random variable, and let represent theprobability.
-Five cards are drawn from a deck. The number of tens is counted.
(Multiple Choice)
4.9/5  (30)
(30)
A die is rolled five times and the number of fours that come up is tallied. Find the probability of getting the given result.
-Exactly two fours
(Multiple Choice)
4.9/5  (31)
(31)
Use the payoff matrix to determine the best strategy.
-A computer manufacturer must decide whether or not to market a new product. The new product may or may not be better than the old product. If they market the new product and it is better than the old product, their sales should increase. If they market the new product and it is not better, they will lose money to competitors. If they do not market the new product, they will lose to competitors if it is actually better and will lose just the research costs if it is not better. The manufacturer estimates that the pay off matrix is as follows:
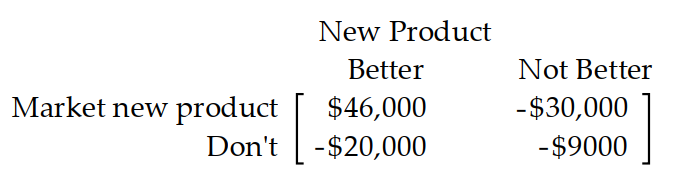 What should the manufacturer do if he is a pessimist?
What should the manufacturer do if he is a pessimist?
(Multiple Choice)
4.9/5  (33)
(33)
Find the expected value of the random variable in the experiment.
-Three coins are tossed, and the number of tails is noted.
(Multiple Choice)
4.8/5  (26)
(26)
Solve the problem.
-The library is to be given 8 books as a gift. The books will be selected from a list of 20 titles. If each book selected must have a different title, how many possible selections are there?
(Multiple Choice)
4.9/5  (32)
(32)
Solve the problem.
-How many ways can an IRS auditor select 6 of 12 tax returns for an audit?
(Multiple Choice)
4.8/5  (26)
(26)
Prepare a payoff matrix
-A computer manufacturer must decide whether or not to market a new product. The new product may or may not be better than the old product. If the new product is better and the manufacturer markets it, sales should increase by . If they market the new product and it is not better, they will lose to competitors. If the new product is not better than the old product and they do not market it, they will lose just the research costs of . If the new product is better than the old product and they do not market it, they will lose . Prepare a payoff matrix.
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-Amy has 5 blue, 2 red, and 3 green books to arrange on a shelf. In how many ways can the books be arranged if books of the same color are identical and must be grouped together?
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-Experience shows that a ski lodge will be full (174 guests) if there is a heavy snow fall in December, while only partially full (59 guests) with a light snow fall. What is the expected number of guests if the probability for a heavy snow fall is .40 ?
(Multiple Choice)
4.8/5  (36)
(36)
Prepare a payoff matrix
-A clothing manufacturer must decide which of two clothing lines to emphasize for the spring season, her usual line or a budget line. Her success with each line depends on the state of the economy next year. If she emphasizes the budget line, she will make a profit of if the economy is strong, a profit of if the economy is weak, and a profit of if the economy is in-between. If she emphasizes the usual line, she will make a profit of if the economy is strong, a profit of if the economy is weak, and a profit of if the economy is in-between. Prepare a payoff matrix.
(Multiple Choice)
4.8/5  (41)
(41)
Find the requested long-range probabilities based on the transition matrix or data given.
-In one town there are only two cello teachers. In a given semester, the probability that a student will switch from Carol Mosely to Betty Roberts is 0.5 The probability that a student of Betty Roberts will switch to Carol Mosely is 0.1. Find the long-range prediction for the proportion of students with each teacher.
(Multiple Choice)
4.9/5  (34)
(34)
Find the requested long-range probabilities based on the transition matrix or data given.
-At a liberal arts college, students are classified as humanities or science majors. There is a probability of 0.8 that a humanities major will change to science and of 0.3 that a science major will change to humanities. Find the long-range prediction for the proportion of students in each major.
(Multiple Choice)
4.9/5  (37)
(37)
Give the probability distribution and sketch the histogram.
-A class of 44 students took a 10 -point quiz. The frequency of scores is given in the table.
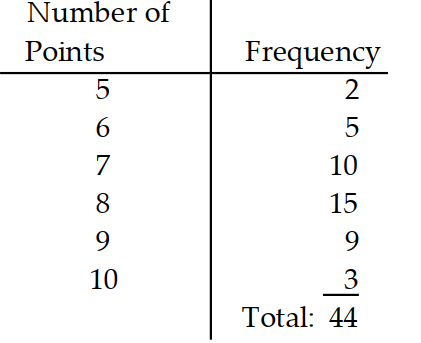
(Multiple Choice)
4.8/5  (40)
(40)
Showing 181 - 200 of 210
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)