Question 1

Find the probability of the event.
-A die is rolled 18 times and two threes come up.

Accepted Answer

A) .160 
B)  .060 
C)  .099 
D)  .230 
A) .160 
B)  .060 
C)  .099 
D)  .230

Question 2

Find the equilibrium vector for the transition matrix.
-$\left[\begin{array}{ll} 0.74 & 0.26 \
0)31 & 0.69
\end{array}\right]$

Accepted Answer

A)  $\left[\begin{array}{ll}0.456 & 0.544\end{array}\right]$ 
B)  $[0.7050 .295]$ 
C)  $\left[\begin{array}{ll}0.544 & 0.456]\end{array}\right.$ 
D)  $\left[\begin{array}{ll}0.295 & 0.705\end{array}\right]$ 
A)  $\left[\begin{array}{ll}0.456 & 0.544\end{array}\right]$ 
B)  $[0.7050 .295]$ 
C)  $\left[\begin{array}{ll}0.544 & 0.456]\end{array}\right.$ 
D)  $\left[\begin{array}{ll}0.295 & 0.705\end{array}\right]$

Question 3

Solve the problem.
-What is the probability that at least 2 of the 435 members of the House of Representatives have the same birthday?

Accepted Answer

A)  1 
B)  .996 
C)  .999 
D)  .995 
A)  1 
B)  .996 
C)  .999 
D)  .995

Question 4

Prepare a probability distribution for the experiment. Let $x$ represent the random variable, and let $P$ represent theprobability.
-Four coins are tossed and the number of heads is counted.

Accepted Answer

A)    
B)    
C)    
D)    
A)    
B)    
C)    
D)

Question 5

For the transition matrix, find the probability that state 2 changes to state 4 after 5 repetitions of the experiment.
-$\left[\begin{array}{lllll}0.2 & 0.1 & 0.1 & 0.4 & 0.2 \ 0.1 & 0.1 & 0.1 & 0.1 & 0.6 \ 0.1 & 0.2 & 0.3 & 0.2 & 0.2 \ 0.2 & 0.2 & 0.1 & 0.4 & 0.1 \ 0.1 & 0.1 & 0.3 & 0.2 & 0.3\end{array}\right]$

Accepted Answer

A)  0.00032 
B)  0.13385 
C)  0.26600 
D)  None of these 
A)  0.00032 
B)  0.13385 
C)  0.26600 
D)  None of these

Question 6

Find the probability of the following card hands-from a 52 card deck. In poker, aces are either high or low. A bridgehand is made up of 13 cards.
-In poker, a straight flush (5 in a row in a single suit, but not a royal flush)

Accepted Answer

A)  $9.23 \times 10^{-6}$ 
B)  $1.39 \times 10^{-5}$ 
C)  $2.31 \times 10^{-6}$ 
D)  $1.23 \times 10^{-5}$ 
A)  $9.23 \times 10^{-6}$ 
B)  $1.39 \times 10^{-5}$ 
C)  $2.31 \times 10^{-6}$ 
D)  $1.23 \times 10^{-5}$

Question 7

Find the probability of the following card hands-from a 52 card deck. In poker, aces are either high or low. A bridgehand is made up of 13 cards.
-A royal flush (5 highest cards of a single suit) in poker

Accepted Answer

A)  $2.75 \times 10^{-4}$ 
B)  $1.54 \times 10^{-6}$ 
C)  $3.85 \times 10^{-7}$ 
D)  $1.98 \times 10^{-3}$ 
A)  $2.75 \times 10^{-4}$ 
B)  $1.54 \times 10^{-6}$ 
C)  $3.85 \times 10^{-7}$ 
D)  $1.98 \times 10^{-3}$

Question 8

Use the payoff matrix to determine the best strategy.
-A backpacker is planning a three-day trip in the backcountry with a friend. She wishes to keep the weight of her pack to a minimum. She has decided to bring either rock climbing shoes or an extra fleece jacket but not both. The fleece jacket will be useful if the weather is cold. The rock climbing shoes will be useful if the weather is warm. In trying to decide which of these two items to bring, the backpacker decides on the utilities shown in the following payoff matrix:
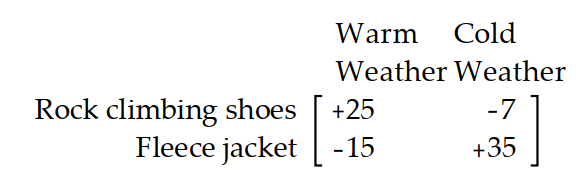  Which of the items should the backpacker bring if the probability of cold weather is 0.4 ?

Accepted Answer

A)  neither 
B)  fleece jacket 
C)  rock climbing shoes 
A)  neither 
B)  fleece jacket 
C)  rock climbing shoes

Question 9

Solve the problem.
-Five cards are drawn at random from an ordinary deck of 52 cards. In how many ways is it possible to draw two red cards and three black cards?

Accepted Answer

A)  422,500 ways 
B)  $1,690,000$ ways 
C)  845,000 ways 
D)  $1,267,500$ ways 
A)  422,500 ways 
B)  $1,690,000$ ways 
C)  845,000 ways 
D)  $1,267,500$ ways

Question 10

A die is rolled 20 times and the number of twos that come up is tallied. Find the probability of getting the given result.
-Exactly two twos

Accepted Answer

A) .116 
B) .198 
C)  .011 
D) .159 
A) .116 
B) .198 
C)  .011 
D) .159

Question 11

A bag contains 6 cherry, 3 orange, and 2 lemon candies. You reach in and take 3 pieces of candy at random. Find the probability.
-All lemon

Accepted Answer

A)  .061 
B)  .1212 
C)  0 
D)  1 
A)  .061 
B)  .1212 
C)  0 
D)  1

Question 12

A bag contains 6 cherry, 3 orange, and 2 lemon candies. You reach in and take 3 pieces of candy at random. Find the probability.
-All orange

Accepted Answer

A)  .0182 
B)  .7272 
C)  .0011 
D)  .0061 
A)  .0182 
B)  .7272 
C)  .0011 
D)  .0061

Question 13

Find the probability of the following card hands-from a 52 card deck. In poker, aces are either high or low. A bridgehand is made up of 13 cards.
-In poker, a full house ( 3 cards of one value, 2 of another value)

Accepted Answer

A)  $6.55 \times 10^{-3}$ 
B)  $3.85 \times 10^{-5}$ 
C)  $1.44 \times 10^{-3}$ 
D)  $9.20 \times 10^{-6}$ 
A)  $6.55 \times 10^{-3}$ 
B)  $3.85 \times 10^{-5}$ 
C)  $1.44 \times 10^{-3}$ 
D)  $9.20 \times 10^{-6}$

Question 14

Find the probability of the following card hands-from a 52 card deck. In poker, aces are either high or low. A bridgehand is made up of 13 cards.
-In bridge, all cards in one suit

Accepted Answer

A)  $3.14 \times 10^{-12}$ 
B)  $3.14 \times 10^{-11}$ 
C)  $6.30 \times 10^{-12}$ 
D)  $1.57 \times 10^{-12}$ 
A)  $3.14 \times 10^{-12}$ 
B)  $3.14 \times 10^{-11}$ 
C)  $6.30 \times 10^{-12}$ 
D)  $1.57 \times 10^{-12}$

Question 15

Solve the problem.
-Find the expected number of boys in a family of 4 children.

Accepted Answer

A)  2.5 
B)  3 
C)  2.75 
D)  2 
A)  2.5 
B)  3 
C)  2.75 
D)  2

Question 16

Find the expected value of the optimal strategy.
-A clothing manufacturer must decide which of two clothing lines to emphasize for the spring season, her usual line or a budget line. Her success with each line depends on the state of the economy next year. She estimates the payoff matrix to be as follows:
 
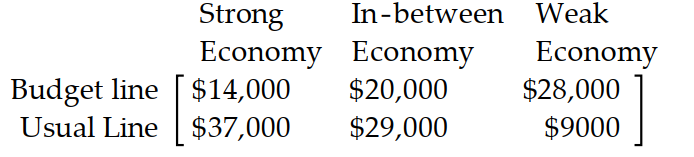Economists believe that there is a 5\% chance of a strong economy next year, a $75 \%$ chance of a weak economy, and a $20 \%$ chance of an in-between economy. What is the manufacturer's maximum expected profit?

Accepted Answer

A)  $\$ 20,667$ 
B)  $\$ 14,400$ 
C)  $\$ 25,000$ 
D)  $\$ 25,700$ 
A)  $\$ 20,667$ 
B)  $\$ 14,400$ 
C)  $\$ 25,000$ 
D)  $\$ 25,700$

Question 17

Solve the problem.
-Amy has 5 blue, 3 red, and 4 green books to arrange on a shelf. In how many ways can the books be arranged if books of the same color must be grouped together? (Assume that books of the same color are distinguishable.)

Accepted Answer

A)  6 
B)  150 
C)  103,680 
D)  17,280 
A)  6 
B)  150 
C)  103,680 
D)  17,280

Question 18

Decide whether or not the transition matrix is regular.
-$\left[\begin{array}{rrr}0.98 & 0 & 0.02 \ 0.83 & 0.17 & 0 \ 0 & 0.57 & 0.43\end{array}\right]$

Accepted Answer

A) True 
 B)False

Question 19

Provide an appropriate response.
-Identify each of the variables in the Binomial Probability Formula.
$\mathrm{P}(\mathrm{x})=\frac{\mathrm{n} !}{(\mathrm{n}-\mathrm{x}) ! \mathrm{x} !} \cdot \mathrm{p}^{\mathrm{x}} \cdot \mathrm{q}^{\mathrm{n}-\mathrm{x}}$
Also, explain what the fraction $\frac{n !}{(n-x) ! x !}$ computes.

Accepted Answer

n is the fixed number of trials, x is th

Question 20

Find the requested probability.
-A child rolls a 6 -sided die 6 times. What is the probability of the child rolling exactly three sixes?

Accepted Answer

A)  .4441 
B)  .5362 
C)  .0594 
D) .0536 
A)  .4441 
B)  .5362 
C)  .0594 
D) .0536

Find the probability of the event. -A die is rolled 18 times and two threes come up.

Find the equilibrium vector for the transition matrix. - $\left[\begin{array}{ll} 0.74 & 0.26 \\0)31 & 0.69\end{array}\right]$

Solve the problem. -What is the probability that at least 2 of the 435 members of the House of Representatives have the same birthday?

Prepare a probability distribution for the experiment. Let $x$ represent the random variable, and let $P$ represent theprobability. -Four coins are tossed and the number of heads is counted.

Find the probability of the following card hands-from a 52 card deck. In poker, aces are either high or low. A bridgehand is made up of 13 cards. -In poker, a straight flush (5 in a row in a single suit, but not a royal flush)

Find the probability of the following card hands-from a 52 card deck. In poker, aces are either high or low. A bridgehand is made up of 13 cards. -A royal flush (5 highest cards of a single suit) in poker

Solve the problem. -Five cards are drawn at random from an ordinary deck of 52 cards. In how many ways is it possible to draw two red cards and three black cards?

A die is rolled 20 times and the number of twos that come up is tallied. Find the probability of getting the given result. -Exactly two twos

A bag contains 6 cherry, 3 orange, and 2 lemon candies. You reach in and take 3 pieces of candy at random. Find the probability. -All lemon

A bag contains 6 cherry, 3 orange, and 2 lemon candies. You reach in and take 3 pieces of candy at random. Find the probability. -All orange

Find the probability of the following card hands-from a 52 card deck. In poker, aces are either high or low. A bridgehand is made up of 13 cards. -In poker, a full house ( 3 cards of one value, 2 of another value)

Find the probability of the following card hands-from a 52 card deck. In poker, aces are either high or low. A bridgehand is made up of 13 cards. -In bridge, all cards in one suit

Solve the problem. -Find the expected number of boys in a family of 4 children.

Solve the problem. -Amy has 5 blue, 3 red, and 4 green books to arrange on a shelf. In how many ways can the books be arranged if books of the same color must be grouped together? (Assume that books of the same color are distinguishable.)

Decide whether or not the transition matrix is regular. - $\left[\begin{array}{rrr}0.98 & 0 & 0.02 \\ 0.83 & 0.17 & 0 \\ 0 & 0.57 & 0.43\end{array}\right]$

Find the requested probability. -A child rolls a 6 -sided die 6 times. What is the probability of the child rolling exactly three sixes?

Algebra and Equations

Graphs, Lines, and Inequalities

Functions and Graphs

Exponential and Logarithmic Functions

Mathematics of Finance

Systems of Linear Equations and Matrices

Linear Programming

Sets and Probability

Introduction to Statistics

Differential Calculus

Applications of the Derivative

Integral Calculus

Multivariate Calculus

Filters

Exam 9: Counting, Probability Distributions, and Further Topics in Probability