Exam 9: Counting, Probability Distributions, and Further Topics in Probability
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Use the payoff matrix to determine the best strategy.
-A computer manufacturer must decide whether or not to market a new product. The new product may or may not be better than the old product. If they market the new product and it is better than the old product, their sales should increase. If they market the new product and it is not better, they will lose money to competitors. If they do not market the new product, they will lose to competitors if it is actually better and will lose just the research costs if it is not better. The manufacturer estimates that the payoff matrix is as follows:
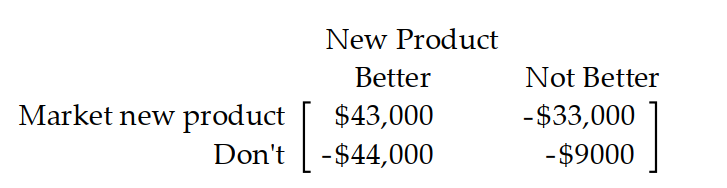 What should the manufacturer do if he is an optimist?
What should the manufacturer do if he is an optimist?
(Multiple Choice)
4.9/5  (39)
(39)
Find the expected value of the optimal strategy.
-A farmer must decide on which of two pieces of land to grow his crops. The first piece of land has better soil and will yield a larger harvest. However this piece of land is low lying and is coastal and his crops will be destroyed in the event of a storm and flooding. The second piece of land has poorer soil and will yield a smaller harvest but is at a higher elevation and would not be affected by flooding. He estimates that the payoff matrix is as follows:
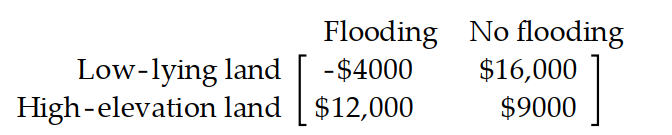 Based on meteorological records from previous years, the farmer estimates the probability of flooding next year to be 0.15 . What is the farmer's expected profit if he picks the best strategy?
Based on meteorological records from previous years, the farmer estimates the probability of flooding next year to be 0.15 . What is the farmer's expected profit if he picks the best strategy?
(Multiple Choice)
4.8/5  (38)
(38)
Sketch a transition diagram for the given transition matrix.
-
(Multiple Choice)
4.8/5  (37)
(37)
Prepare a probability distribution for the experiment. Let represent the random variable, and let represent theprobability.
-A field goal kicker has a kicking average of .75 and he tries 3 field goals in a game. The number of field goals is counted.
(Multiple Choice)
4.9/5  (36)
(36)
Find the expected value for the random variable.
-For a certain animal species, the probability that a female will have a certain number of offspring in a given year is given in the table below. Find the expected number of offspring per year.
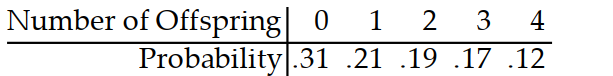
(Multiple Choice)
4.8/5  (37)
(37)
A die is rolled 20 times and the number of twos that come up is tallied. Find the probability of getting the given result.
-Exactly five twos
(Multiple Choice)
4.8/5  (30)
(30)
Solve the problem.
-Awards are to be presented to seven people: Jeff, Karen, Lyle, Maria, Norm, Olivia, and Paul. How many different orders are possible for the awards if the men are to receive their awards first, and then the women?
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-Find the number of ways of arranging 5 distinct items in a circle.
(Multiple Choice)
4.7/5  (29)
(29)
Solve the problem.
-Suppose you pay to roll a fair die with the understanding that you will get back for rolling a 1 or a 5 , nothing otherwise. What are your expected winnings?
(Multiple Choice)
4.8/5  (37)
(37)
Find the requested long-range probabilities based on the transition matrix or data given.
-Weather is classified as sunny or cloudy in a certain place. The probability that it will be sunny on a given day depends on whether it was sunny the previous day. The transition matrix is given below. Find the long-range prediction for the proportion of sunny and cloudy days.
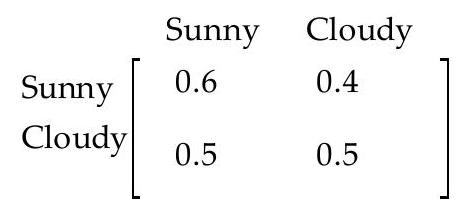
(Multiple Choice)
4.9/5  (33)
(33)
Give the probability distribution and sketch the histogram.
-The telephone company kept track of the calls for the correct time during a 24 -hour period for two weeks. The results are shown in the table.
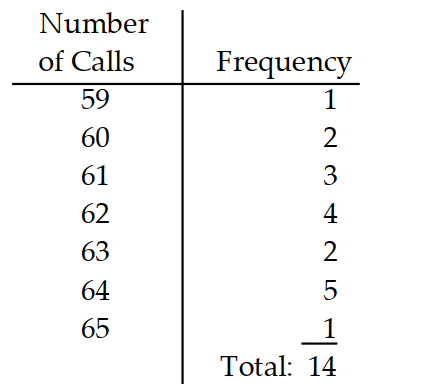
(Multiple Choice)
4.8/5  (36)
(36)
Provide an appropriate response.
-Suppose that a class of 30 students is assigned to write an essay.
1) Suppose 4 essays are randomly chosen to appear on the class bulletin board. How many different groups of 4 are possible?
2) Suppose 4 essays are randomly chosen for awards of $10, $7, $5, and $3. How many different groups of 4 are possible?
Explain the significant differences between problems 1 and 2.
(Essay)
4.7/5  (32)
(32)
Solve the problem.
-Find the number of ways of arranging 8 distinct items in a circle.
(Multiple Choice)
4.8/5  (41)
(41)
Showing 81 - 100 of 210
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)